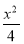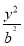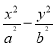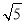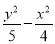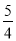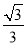题目内容
已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则|AB|·|CD|的值正确的是( ).
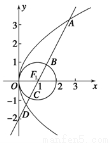
A.等于1 B.最小值是1 C.等于4 D.最大值是4
A
【解析】设直线l:x=ty+1,代入抛物线方程,
得y2-4ty-4=0.设A(x1,y1),D(x2,y2),
根据抛物线定义|AF|=x1+1,|DF|=x2+1,
故|AB|=x1,|CD|=x2,所以|AB|·|CD|=x1x2=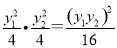 ,
,
而y1y2=-4,代入上式,得|AB|·|CD|=1.故选A.

练习册系列答案
相关题目
随机询问100名性别不同的大学生是否爱好踢毽子运动,得到如下的列联表:
| 男 | 女 | 总计 |
爱好 | 10 | 40 | 50 |
不爱好 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
附表:
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算,统计量K2=4.762,参照附表,得到的正确结论是( ).
A.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C.有97.5%以上的把握认为“爱好该项运动与性别有关”
D.有97.5%以上的把握认为“爱好该项运动与性别无关”