题目内容
已知M是曲线y=ln x+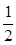 x2+(1-a)x上的一点,若曲线在M处的切线的倾斜角是均不小于
x2+(1-a)x上的一点,若曲线在M处的切线的倾斜角是均不小于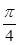 的锐角,则实数a的取值范围是________.
的锐角,则实数a的取值范围是________.
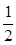 x2+(1-a)x上的一点,若曲线在M处的切线的倾斜角是均不小于
x2+(1-a)x上的一点,若曲线在M处的切线的倾斜角是均不小于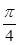 的锐角,则实数a的取值范围是________.
的锐角,则实数a的取值范围是________.(-∞,2]
试题分析:
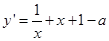 ,因为曲线在M处的切线的倾斜角是均不小于
,因为曲线在M处的切线的倾斜角是均不小于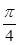 的锐角,所以
的锐角,所以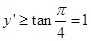 对于任意的
对于任意的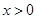 恒成立,即
恒成立,即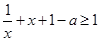
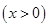 恒成立,所以
恒成立,所以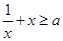 ,而
,而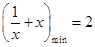 ,故
,故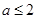 ,所以a的取值范围是
,所以a的取值范围是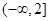 .
.
练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
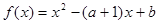 ,
,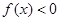 的解集是
的解集是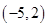 ,求
,求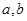 的值;
的值;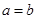 ,解关于
,解关于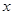 的不等式
的不等式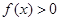 .
.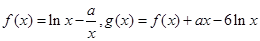 ,其中
,其中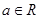 .
.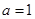 时判断
时判断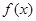 的单调性;
的单调性;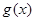 在其定义域为增函数,求正实数
在其定义域为增函数,求正实数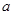 的取值范围;
的取值范围;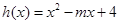 ,当
,当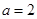 时,若
时,若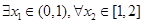 ,总有
,总有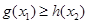 成立,求实数
成立,求实数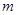 的取值范围.
的取值范围.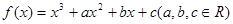 的图像过原点,且在
的图像过原点,且在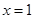 处的切线为直线
处的切线为直线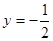
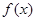 的解析式;
的解析式;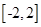 上的最小值和最大值.
上的最小值和最大值.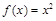 ,
,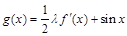 在
在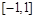 上的减函数.
上的减函数.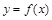 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;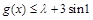 在
在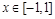 上恒成立,求
上恒成立,求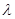 的取值范围;
的取值范围;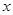 的方程
的方程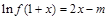 (
(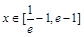 )有两个根(无理数e=2.71828),求m的取值范围.
)有两个根(无理数e=2.71828),求m的取值范围.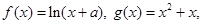 若函数
若函数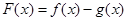 在x = 0处取得极值.
在x = 0处取得极值.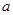 的值;
的值;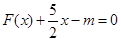 在区间[0,2]上恰有两个不同的实数根,求实数
在区间[0,2]上恰有两个不同的实数根,求实数 的取值范围;
的取值范围;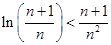 都成立.
都成立.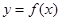 的导函数为
的导函数为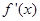 .如果存在
.如果存在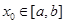 ,使得
,使得 成立,则称
成立,则称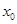 为函数
为函数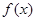 在区间
在区间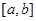 上的“中值点”.那么函数
上的“中值点”.那么函数 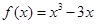 在区间[-2,2]上的“中值点”为____.
在区间[-2,2]上的“中值点”为____.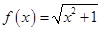 ,对任意
,对任意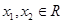 ,恒有
,恒有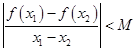 ,其中M是常数,则M的最小值是 .
,其中M是常数,则M的最小值是 .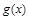 为三次函数
为三次函数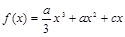 的导函数,则函数
的导函数,则函数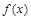 的图像可能是( )
的图像可能是( )