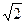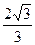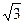题目内容
已知点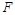 ,
,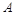 分别为双曲线
分别为双曲线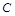 :
: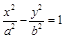
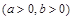 的左焦点、右顶点,点
的左焦点、右顶点,点
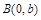 满足
满足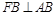 ,则双曲线的离心率为
,则双曲线的离心率为
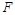 ,
,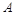 分别为双曲线
分别为双曲线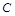 :
: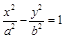
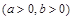 的左焦点、右顶点,点
的左焦点、右顶点,点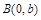 满足
满足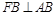 ,则双曲线的离心率为
,则双曲线的离心率为A.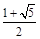 | B.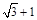 | C.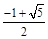 | D.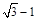 |
A
本题考查的知识点是平面向量的数量积运算及双曲线的简单性质,由 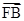 ?
? 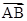 =0,可得FB⊥AB,易得RT△AOB∽RT△BOF,由相似三角形的性质及根据双曲线的定义,即可找到a与c之间的数量关系,进而求出离心率e.要求双曲线的离心率,关键是根据已知条件
=0,可得FB⊥AB,易得RT△AOB∽RT△BOF,由相似三角形的性质及根据双曲线的定义,即可找到a与c之间的数量关系,进而求出离心率e.要求双曲线的离心率,关键是根据已知条件
解答:解:如图,
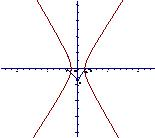
∵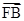 ?
? 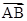 =0
=0
∴FB⊥AB,
则RT△AOB∽RT△BOF,
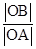 =
=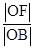 ?
?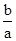 =
=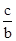
即b2=ac
∴c2-a2=ac两边同除ac得
e2-1=e
即e2-e-1=0,
解得:e=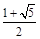 或e=
或e=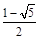 (舍去)
(舍去)
∴e=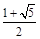
故答案为A
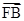 ?
? 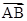 =0,可得FB⊥AB,易得RT△AOB∽RT△BOF,由相似三角形的性质及根据双曲线的定义,即可找到a与c之间的数量关系,进而求出离心率e.要求双曲线的离心率,关键是根据已知条件
=0,可得FB⊥AB,易得RT△AOB∽RT△BOF,由相似三角形的性质及根据双曲线的定义,即可找到a与c之间的数量关系,进而求出离心率e.要求双曲线的离心率,关键是根据已知条件解答:解:如图,

∵
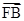 ?
? 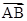 =0
=0∴FB⊥AB,
则RT△AOB∽RT△BOF,
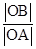 =
=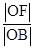 ?
?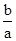 =
=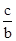
即b2=ac
∴c2-a2=ac两边同除ac得
e2-1=e
即e2-e-1=0,
解得:e=
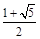 或e=
或e=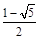 (舍去)
(舍去)∴e=
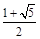
故答案为A

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
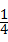
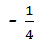
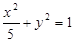 共焦点,且一条渐近线方程是
共焦点,且一条渐近线方程是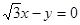 ,则此双曲
,则此双曲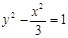 B.
B.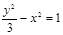 C.
C.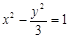 D.
D.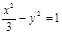
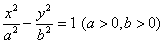 的一个焦点
的一个焦点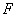 作渐近线的垂线
作渐近线的垂线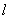 ,垂足为
,垂足为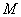 ,
,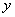 轴于点
轴于点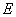 ,若
,若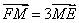 ,则该双曲线的离心率为 .
,则该双曲线的离心率为 . 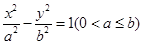 的离心率为e,则e的取值范围是( )
的离心率为e,则e的取值范围是( )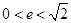
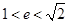
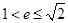
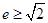
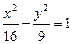 上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则| PQ |-| PR | 的最大值是 .
上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则| PQ |-| PR | 的最大值是 .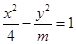 的焦距为
的焦距为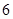 , 则
, 则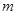 的值等于( )
的值等于( )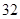

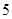
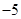
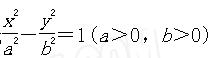 的左、右焦点,若双曲线左支上存在一点P使得
的左、右焦点,若双曲线左支上存在一点P使得 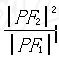 =8a,则双曲线的离心率的取值范围是
=8a,则双曲线的离心率的取值范围是 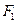 、
、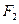 在
在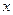 轴上,A为双曲线上一点,
轴上,A为双曲线上一点, 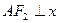 轴,
轴, 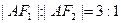 ,则双曲线的离心率为( )
,则双曲线的离心率为( )