题目内容
已知双曲线 (a>0,b>0)的离心率
(a>0,b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离是
,过点A(0,-b)和B(a,0)的直线与原点的距离是 .
.
(Ⅰ)求双曲线的方程及渐近线方程;
(Ⅱ)若直线y=kx+5 (k≠0)与双曲线交于不同的两点C、D,且两点都在以A为圆心的同一个圆上,求k的值.
 (a>0,b>0)的离心率
(a>0,b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离是
,过点A(0,-b)和B(a,0)的直线与原点的距离是 .
.(Ⅰ)求双曲线的方程及渐近线方程;
(Ⅱ)若直线y=kx+5 (k≠0)与双曲线交于不同的两点C、D,且两点都在以A为圆心的同一个圆上,求k的值.
(Ⅰ)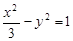 ,
,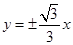 ;(Ⅱ)
;(Ⅱ)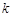 =
=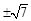
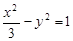 ,
,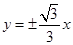 ;(Ⅱ)
;(Ⅱ)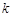 =
=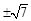
试题分析:本题主要考察双曲线的标准方程、韦达定理等基础知识,考察学生运算能力、综合分析和解决问题的能力.(Ⅰ)离心率为
 ,∴
,∴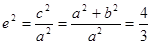 ,∴
,∴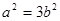 ①,直线
①,直线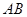 的方程为
的方程为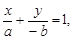 即
即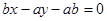 ,利用点到直线的距离公式得到:
,利用点到直线的距离公式得到: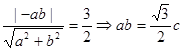 ②,两式联立,可求出
②,两式联立,可求出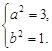 ,∴双曲线方程为
,∴双曲线方程为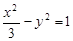 ,渐近线方程为:
,渐近线方程为: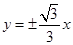 ;(Ⅱ)
;(Ⅱ)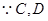 两点在以
两点在以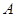 为圆心的同一个圆上,
为圆心的同一个圆上,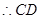 的中垂线过点
的中垂线过点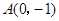 ,将直线
,将直线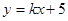 与双曲线
与双曲线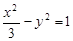 联立,消去
联立,消去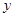 ,可得
,可得 ,设
,设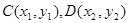 ,中点为
,中点为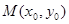 ,则
,则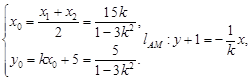 ∴
∴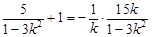 ,解得
,解得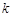 =
=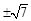 ,并检验是否满足(
,并检验是否满足(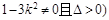 .
.试题解析:(Ⅰ)直线
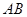 的方程为:
的方程为: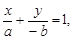 即
即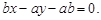
又原点
 到直线
到直线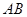 的距离
的距离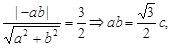
由
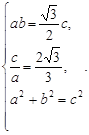 得
得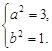 3分
3分所求双曲线方程为
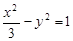 4分
4分(注:也可由面积法求得
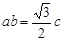 )
)渐近线方程为:
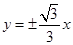 5分
5分(Ⅱ)方法1:由(1)可知
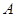 (0,-1),设
(0,-1),设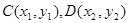 ,由
,由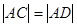
得:
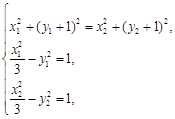 7分
7分∴3+3
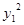 +
+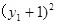 =3+3
=3+3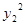 +
+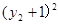 ,
,整理得:
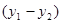
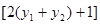 =0,
=0, ∵
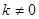 ,∴
,∴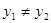 ,∴
,∴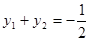 ,
, 又由
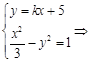
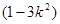
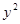 -10
-10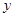 +25-3
+25-3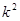 =0 (
=0 (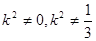 ),
),∴y+y2=
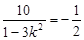 , 10分
, 10分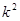 =7, 11分
=7, 11分由△=100-4(1-3
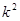 )(25-3
)(25-3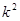 )>0
)>0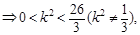
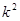 =7满足此条件,
=7满足此条件,满足题设的
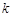 =
=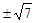 . 12分
. 12分方法2:设
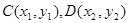 ,中点为
,中点为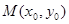 ,
,由
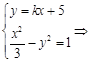
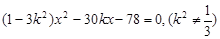 , 7分
, 7分∵
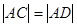 ,
,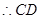 的中垂线过点
的中垂线过点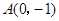 9分
9分∵
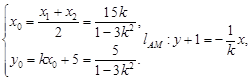 ∴
∴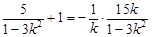 11分
11分整理得
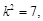 解得
解得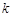 =
=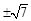 .(
.(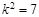 满足
满足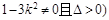 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
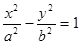 (
(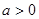 ,
,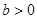 )满足
)满足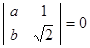 ,且双曲线的右焦点与抛物线
,且双曲线的右焦点与抛物线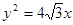 的焦点重合,则该双曲线的方程为______________.
的焦点重合,则该双曲线的方程为______________.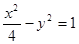 的两个焦点,点P在双曲线上满足∠F1PF2=90°,那么△F1PF2的面积是( )
的两个焦点,点P在双曲线上满足∠F1PF2=90°,那么△F1PF2的面积是( )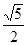
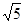
 的一条渐近线与直线2x+y+1=0垂直,则这双曲线的离心率为 ( )
的一条渐近线与直线2x+y+1=0垂直,则这双曲线的离心率为 ( )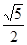

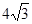

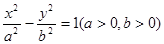 的右焦点为
的右焦点为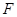 ,过
,过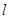 交双曲线的渐近线于
交双曲线的渐近线于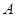 ,
,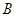 两点,且与其中一条渐近线垂直,若
两点,且与其中一条渐近线垂直,若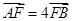 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )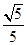
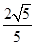
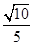
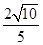
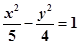 的顶点和焦点到其渐近线距离的比是( )
的顶点和焦点到其渐近线距离的比是( )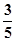
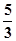
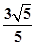
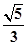
 的离心率为
的离心率为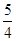 , 则m等于 .
, 则m等于 .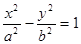 的渐近线方程是
的渐近线方程是 ,那么此双曲线的离心率为 .
,那么此双曲线的离心率为 .