题目内容
(1)计算:1.10+
-0.5-2+lg25+2lg2
(2)解不等式:loga(2x+3)>loga(5x-6)(其中a>0且a≠1)
| 3 | 216 |
(2)解不等式:loga(2x+3)>loga(5x-6)(其中a>0且a≠1)
分析:(1)利用对数的运算性质求得1.10+
-0.5-2+lg25+2lg2 的值.
(2)当a>1时,原不等式等价于
,由此求得原不等式的解集.当 0<a<1时,原不等式等价于
,由此求得原
不等式的解集.
| 3 | 216 |
(2)当a>1时,原不等式等价于
|
|
不等式的解集.
解答:解:(1)1.10+
-0.5-2+lg25+2lg2=1+6-4+lg100=3+2=5.
(2)当a>1时,原不等式等价于
,解得
<x<3,所以原不等式的解集是(
,3).
当 0<a<1时,原不等式等价于
,解得 x>3,故原不等式的解集是(3,+∞).
综上可得,当a>1时,原不等式的解集是(
,3); 当 0<a<1时,原不等式的解集是(3,+∞).
| 3 | 216 |
(2)当a>1时,原不等式等价于
|
| 6 |
| 5 |
| 6 |
| 5 |
当 0<a<1时,原不等式等价于
|
综上可得,当a>1时,原不等式的解集是(
| 6 |
| 5 |
点评:本题主要考查对数的运算性质,对数函数的定义域、单调性和特殊点,体现了等价转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
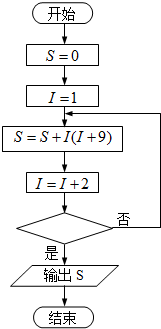 某同学设计如图的流程图用以计算和式1×10+3×12+5×14+…+19×28的值,则在判断框中可以填写( )
某同学设计如图的流程图用以计算和式1×10+3×12+5×14+…+19×28的值,则在判断框中可以填写( )