题目内容
点P在以F1、F2为焦点的椭圆
+
=1上运动，则△F1F2P的重心G的轨迹方程是
+y2=1（x≠0）
+y2=1（x≠0）．
| x2 |
| 16 |
| y2 |
| 9 |
| 9x2 |
| 16 |
| 9x2 |
| 16 |
分析：求出椭圆
+
=1的焦点为F1（-
，0），F2（
，0）．设G（x，y），P（m，n），根据三角形重心坐标公式建立关系式，解出m=3x且n=3y，利用点P（m，n）在椭圆上代入题中椭圆方程，化简即可得到所求△F1F2P的重心G的轨迹方程．
| x2 |
| 16 |
| y2 |
| 9 |
| 7 |
| 7 |
解答：解：设G（x，y），P（m，n），则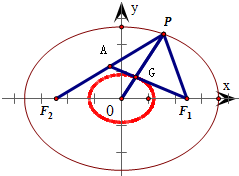
∵椭圆
+
=1中，a=4，b=3，
∴c=
=
，
得椭圆的焦点为F1（-
，0），F2（
，0），
∵G为△PF1F2的重心，
∴x=
（-
+
+m）=
m，y=
（0+0+n）=
n
解之得m=3x，n=3y
∵点P在椭圆
+
=1上运动，得
+
=1
∴将m=3x、n=3y代入，得
+
=1，即
+y2=1
∵P、F1、F2三点不共线，可得x≠0
∴△PF1F2的重心G的轨迹方程是
+y2=1，（x≠0）
故答案为：
+y2=1（x≠0）
∵椭圆
| x2 |
| 16 |
| y2 |
| 9 |
∴c=
| 16-9 |
| 7 |
得椭圆的焦点为F1（-
| 7 |
| 7 |
∵G为△PF1F2的重心，
∴x=
| 1 |
| 3 |
| 7 |
| 7 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解之得m=3x，n=3y
∵点P在椭圆
| x2 |
| 16 |
| y2 |
| 9 |
| m2 |
| 16 |
| n2 |
| 9 |
∴将m=3x、n=3y代入，得
| 9x2 |
| 16 |
| 9y2 |
| 9 |
| 9x2 |
| 16 |
∵P、F1、F2三点不共线，可得x≠0
∴△PF1F2的重心G的轨迹方程是
| 9x2 |
| 16 |
故答案为：
| 9x2 |
| 16 |
点评：本题给出椭圆的焦点三角形，求三角形的重心G的轨迹方程．着重考查了椭圆的标准方程、三角形的重心坐标和动点轨迹方程的求法等知识，属于中档题．
练习册系列答案
相关题目
（2013•深圳一模）已知两点F1（-1，0）及F2（1，0），点P在以F1、F2为焦点的椭圆C上，且|PF1|、|F1F2|、|PF2|构成等差数列．