题目内容
函数f(x)=2cos2x+sin2x-1,给出下列四个命题:①函数在区间
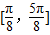 上是减函数;
上是减函数;②直线
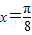 是函数图象的一条对称轴;
是函数图象的一条对称轴;③函数f(x)的图象可由函数
 的图象向左平移
的图象向左平移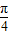 个单位长度而得到;
个单位长度而得到;④若
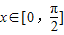 ,则f(x)的值域是
,则f(x)的值域是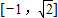 .
.其中所有正确命题的序号是 .
【答案】分析:化简函数为同角同名函数,利用2cos2x-1=cos2x,sin2x+cos2x=)=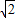 sin(2x+
sin(2x+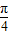 ).再利用正弦函数的性质,对称轴方程x=kπ+
).再利用正弦函数的性质,对称轴方程x=kπ+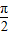 ,k∈z;递减区间为[2kπ+
,k∈z;递减区间为[2kπ+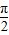 ,2kπ+
,2kπ+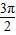 ],k∈z,及函数图象的变化规律解决.
],k∈z,及函数图象的变化规律解决.
解答:解:首先对函数进行化简,f(x)=2cos2x+sin2x-1=sin2x+cos2x=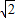 (sin2xcos
(sin2xcos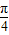 +cos2xsin
+cos2xsin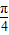 )=
)=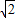 sin(2x+
sin(2x+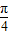 ).
).
对①,令2x+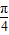 =kπ+
=kπ+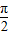 ,得对称轴方程x=
,得对称轴方程x=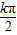 +
+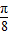 ,k∈z,∴②正确;
,k∈z,∴②正确;
对①,令2kπ+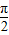 <2x+
<2x+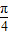 <2kπ+
<2kπ+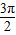 ,得 kπ+
,得 kπ+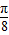 <x<kπ+
<x<kπ+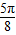 ,k∈z.函数的递减区间为[kπ+
,k∈z.函数的递减区间为[kπ+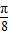 ,kπ+
,kπ+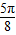 ],k∈z,∴①√;
],k∈z,∴①√;
对③,平移的单位应是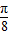 ,∴③×.
,∴③×.
对④,当x∈[0,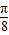 ]时f(x)单调递增,当x∈[
]时f(x)单调递增,当x∈[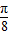 ,
,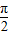 ]时单调递减,f(
]时单调递减,f(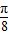 )=
)=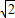 ,f(
,f(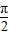 )=-1∴值域是[-1,
)=-1∴值域是[-1,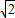 ],∴④√.
],∴④√.
故答案是①②④
点评:牢记三角函数的性质及图象变化规律,利用整体代入求解复合函数的对称轴、单调区间、值域是本题的关键.
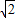 sin(2x+
sin(2x+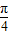 ).再利用正弦函数的性质,对称轴方程x=kπ+
).再利用正弦函数的性质,对称轴方程x=kπ+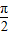 ,k∈z;递减区间为[2kπ+
,k∈z;递减区间为[2kπ+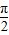 ,2kπ+
,2kπ+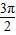 ],k∈z,及函数图象的变化规律解决.
],k∈z,及函数图象的变化规律解决.解答:解:首先对函数进行化简,f(x)=2cos2x+sin2x-1=sin2x+cos2x=
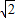 (sin2xcos
(sin2xcos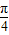 +cos2xsin
+cos2xsin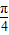 )=
)=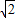 sin(2x+
sin(2x+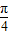 ).
).对①,令2x+
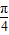 =kπ+
=kπ+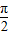 ,得对称轴方程x=
,得对称轴方程x=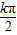 +
+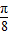 ,k∈z,∴②正确;
,k∈z,∴②正确;对①,令2kπ+
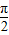 <2x+
<2x+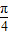 <2kπ+
<2kπ+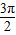 ,得 kπ+
,得 kπ+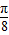 <x<kπ+
<x<kπ+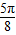 ,k∈z.函数的递减区间为[kπ+
,k∈z.函数的递减区间为[kπ+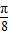 ,kπ+
,kπ+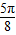 ],k∈z,∴①√;
],k∈z,∴①√;对③,平移的单位应是
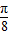 ,∴③×.
,∴③×.对④,当x∈[0,
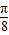 ]时f(x)单调递增,当x∈[
]时f(x)单调递增,当x∈[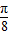 ,
,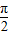 ]时单调递减,f(
]时单调递减,f(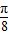 )=
)=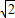 ,f(
,f(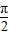 )=-1∴值域是[-1,
)=-1∴值域是[-1,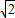 ],∴④√.
],∴④√.故答案是①②④
点评:牢记三角函数的性质及图象变化规律,利用整体代入求解复合函数的对称轴、单调区间、值域是本题的关键.

练习册系列答案
相关题目