题目内容
已知函数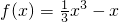
在区间（a2-5，a+1）上有最大值，则实数a的取值范围是
- A.（0，2）
- B.（-2，2）
- C.（-2，1]
- D.（0，1]
B
分析：利用导数求出函数f（x）的极大值点，由题意借助图象可知极大值点在区间（a2-5，a+1）内，由此可得关于a的不等式，解出即可．
解答：f′（x）=x2-1=（x+1）（x-1），
令f′（x）=0得x=-1或x=1，
当x＜-1或x＞1时，f′（x）＞0，当-1＜x＜1时，f′（x）＜0，
所以当x=-1时f（x）取得极大值，当x=1时f（x）取得极小值，
要使f（x）在区间（a2-5，a+1）上有最大值，只需a2-5＜-1＜a+1，解得-2＜a＜2，
所以实数a的取值范围是（-2，2），
故选B．
点评：本题考查利用导数求函数在闭区间上的最值及函数在某点取得极值的条件，考查数形结合思想，属中档题．
分析：利用导数求出函数f（x）的极大值点，由题意借助图象可知极大值点在区间（a2-5，a+1）内，由此可得关于a的不等式，解出即可．
解答：f′（x）=x2-1=（x+1）（x-1），
令f′（x）=0得x=-1或x=1，
当x＜-1或x＞1时，f′（x）＞0，当-1＜x＜1时，f′（x）＜0，
所以当x=-1时f（x）取得极大值，当x=1时f（x）取得极小值，
要使f（x）在区间（a2-5，a+1）上有最大值，只需a2-5＜-1＜a+1，解得-2＜a＜2，
所以实数a的取值范围是（-2，2），
故选B．
点评：本题考查利用导数求函数在闭区间上的最值及函数在某点取得极值的条件，考查数形结合思想，属中档题．
练习册系列答案
相关题目
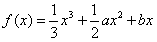在区间[－1，1)，(1，3]内各有一个极值点．
在区间[-1，1），（1，3]内各有一个极值点。
在区间[-1，1），（1，3]内各有一个极值点．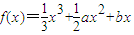
在区间[-1，1），（1，3]内各有一个极值点．