题目内容
如图,在正方体ABCD―A1B1C1D1中,点E是DD1的中点.
(1)求证:AC⊥BD1;
(2)求证:BD1∥平面CEA.
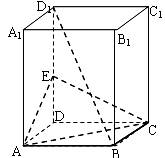
证:(1)∵棱柱ABCD―A1B1C1D1为正方体,∴D1D⊥面ABCD,
∴BD是BD1在底面ABCD内的射影。又∵BD⊥AC,∴BD1⊥AC。
(2)设AC∩BD = O,连结OE,∵O、E分别为BD、DD1的中点,
∴OE∥BD1.又∵BD1![]() 平面CEA,OE
平面CEA,OE![]() 平面CEA,∴BD1∥平面CEA。
平面CEA,∴BD1∥平面CEA。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )