题目内容
（本小题满分10分）选修4-4：坐标系与参数方程
已知直线的极坐标方程为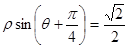
，圆
的参数方程为
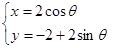（其中
为参数）.
（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆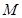上的点到直线的距离的最小值.
已知直线的极坐标方程为
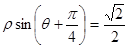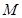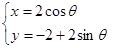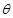，圆的参数方程为（其中为参数）.（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆
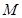上的点到直线的距离的最小值.（Ⅰ）
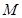（Ⅱ）圆上的点到直线的距离的最小值为
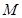（Ⅱ）圆上的点到直线的距离的最小值为本题考查极坐标方程与直角坐标方程，参数方程与普通方程的互化，考查点线距离公式的运用，属于基础题．
（Ⅰ）以极点为原点，极轴为x轴正半轴建立直角坐标系，利用和角的正弦函数，即可求得该直线的直角坐标方程；
（Ⅱ）圆M的普通方程为：x2+（y+2）2=4，求出圆心M（0，-2）到直线x+y-1=0的距离，即可得到圆M上的点到直线的距离的最小值．
解：（Ⅰ）以极点为原点，极轴为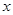
轴正半轴建立直角坐标系. ----------------1分
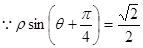
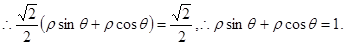----------------2分
所以，该直线的直角坐标方程为：----------------3分
（Ⅱ）圆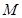的普通方程为：
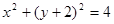----------------4分
圆心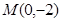
到直线
的距离
---------------5分
所以，圆上的点到直线的距离的最小值为----------------7分
（Ⅰ）以极点为原点，极轴为x轴正半轴建立直角坐标系，利用和角的正弦函数，即可求得该直线的直角坐标方程；
（Ⅱ）圆M的普通方程为：x2+（y+2）2=4，求出圆心M（0，-2）到直线x+y-1=0的距离，即可得到圆M上的点到直线的距离的最小值．
解：（Ⅰ）以极点为原点，极轴为
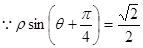
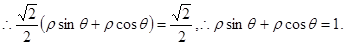轴正半轴建立直角坐标系. ----------------1分----------------2分所以，该直线的直角坐标方程为：
----------------3分（Ⅱ）圆
的普通方程为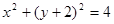：----------------4分圆心
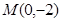到直线的距离---------------5分所以，圆
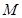上的点到直线的距离的最小值为----------------7分
练习册系列答案
相关题目
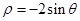的圆心的极坐标是( )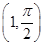
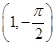
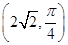作圆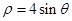
的切线，则切线的极坐标方程是 .
中，圆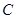
的参数方程为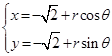
为参数，
．以
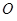为极点，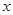
轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线
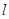的极坐标方程为
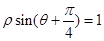．当圆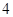
时，圆的半径
．
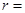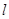经过圆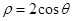
的圆心且与直线
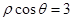平行，则直线
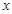轴的正半轴为极轴建坐标系,已知曲线
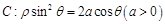,已知过点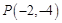
的直线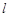
的参数方程为:
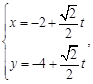直线
分别交于
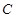和直线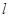
的普通方程;
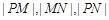成等比数列,求
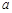的值.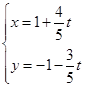 
（
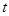为参数）被曲线
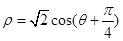所截的弦长.
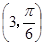，半径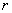
=1，Q点在圆C上运动。
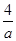，对任意的x∈R恒成立，则实数a的取值范围是 
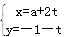（t为参数），圆C∶r=2
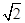cos(q―
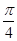)（极轴与x轴的非负半轴重合，且单位长度相同），若直线l被圆C截得弦长为2，则a=