题目内容
已知首项为a(a≠0)的数列{an}的前n项和为Sn,,若对任意的正整数m、n,都有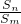 =
=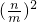 .
.
(Ⅰ)证明:数列{an}是等差数列;
(Ⅱ)若a=1,数列{bn}的首项为b(b≠1),第n(n∈N*,n≥2)项bn是数列{an}的第bn-1项,求证:数列|bn-1|为等比数列;
(Ⅲ)若对(Ⅱ)中的数列{an}和{bn}及任意正整数n,均有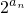 +bn+11≥0成立,求实数b的最小值.
+bn+11≥0成立,求实数b的最小值.
解:(Ⅰ)证明:在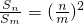 中,取m=1,得
中,取m=1,得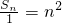 ,即Sn=n2a,
,即Sn=n2a,
当n≥2时,Sn-1=(n-1)2a,
∴an=Sn-Sn-1=n2a-(n-1)2a=(2n-1)a,
当n=1时,a1=a也适合上式,
∴an=(2n-1)a,n∈N+,
∵an+1-an=2a,
∴{an}是以a为首项,2a为公差的等差数列.
(Ⅱ)证明:当a=1时,由(Ⅰ)可得an=2n-1,
∴bn=2bn-1-1,
即有bn-1=2(bn-1-1),
b1-1=b-1≠0,
∴{bn-1}是以b-1为首项,2为公比的等比数列.
(Ⅲ)由(Ⅱ)知,bn-1=(b-1)•2n-1,
∴bn=1+(b-1)•2n-1,
∴由题意得,不等式22n-1+(b-1)•2n-1+12≥0对任意正整数n恒成立,
即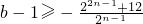 =
=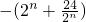 恒成立.
恒成立.
设t=2n(t=2,4,8,…),则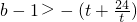 恒成立,
恒成立,
对于函数y=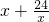 ,
,
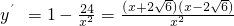 .
.
当x∈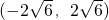 时,y′<0,当x∈
时,y′<0,当x∈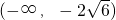 和(2
和(2 ,+∞)时,y′>0,
,+∞)时,y′>0,
∴函数 在
在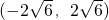 上单调减,在
上单调减,在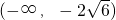 和(2
和(2 ,+∞)上单调增.
,+∞)上单调增.
又当x=4时,y=10;当x=8时,y=11,∴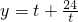 的最小值是10.∴
的最小值是10.∴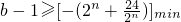 =-10.
=-10.
即b≥-9,
∴实数b的最小值是-9.
分析:(Ⅰ)在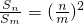 中,取m=1,得
中,取m=1,得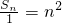 ,即Sn=n2a,所以an=Sn-Sn-1=n2a-(n-1)2a=(2n-1)a,由此能求出{an}是以a为首项,2a为公差的等差数列.
,即Sn=n2a,所以an=Sn-Sn-1=n2a-(n-1)2a=(2n-1)a,由此能求出{an}是以a为首项,2a为公差的等差数列.
(Ⅱ)由an=2n-1,bn=2bn-1-1,知bn-1=2(bn-1-1),由此能够证明|bn-1|都给以b-1为首项,2为公比的等比数列.
(Ⅲ)由bn-1=(b-1)•2n-1,bn=1+(b-1)•2n-1,由题意得,不等式不承认真即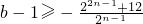 =
=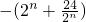 恒成立.
恒成立.
点评:本题考查数列与函数的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件.
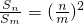 中,取m=1,得
中,取m=1,得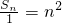 ,即Sn=n2a,
,即Sn=n2a,当n≥2时,Sn-1=(n-1)2a,
∴an=Sn-Sn-1=n2a-(n-1)2a=(2n-1)a,
当n=1时,a1=a也适合上式,
∴an=(2n-1)a,n∈N+,
∵an+1-an=2a,
∴{an}是以a为首项,2a为公差的等差数列.
(Ⅱ)证明:当a=1时,由(Ⅰ)可得an=2n-1,
∴bn=2bn-1-1,
即有bn-1=2(bn-1-1),
b1-1=b-1≠0,
∴{bn-1}是以b-1为首项,2为公比的等比数列.
(Ⅲ)由(Ⅱ)知,bn-1=(b-1)•2n-1,
∴bn=1+(b-1)•2n-1,
∴由题意得,不等式22n-1+(b-1)•2n-1+12≥0对任意正整数n恒成立,
即
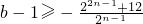 =
=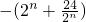 恒成立.
恒成立.设t=2n(t=2,4,8,…),则
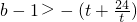 恒成立,
恒成立,对于函数y=
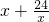 ,
,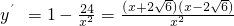 .
.当x∈
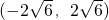 时,y′<0,当x∈
时,y′<0,当x∈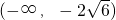 和(2
和(2 ,+∞)时,y′>0,
,+∞)时,y′>0,∴函数
 在
在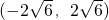 上单调减,在
上单调减,在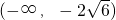 和(2
和(2 ,+∞)上单调增.
,+∞)上单调增.又当x=4时,y=10;当x=8时,y=11,∴
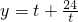 的最小值是10.∴
的最小值是10.∴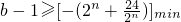 =-10.
=-10.即b≥-9,
∴实数b的最小值是-9.
分析:(Ⅰ)在
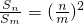 中,取m=1,得
中,取m=1,得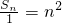 ,即Sn=n2a,所以an=Sn-Sn-1=n2a-(n-1)2a=(2n-1)a,由此能求出{an}是以a为首项,2a为公差的等差数列.
,即Sn=n2a,所以an=Sn-Sn-1=n2a-(n-1)2a=(2n-1)a,由此能求出{an}是以a为首项,2a为公差的等差数列.(Ⅱ)由an=2n-1,bn=2bn-1-1,知bn-1=2(bn-1-1),由此能够证明|bn-1|都给以b-1为首项,2为公比的等比数列.
(Ⅲ)由bn-1=(b-1)•2n-1,bn=1+(b-1)•2n-1,由题意得,不等式不承认真即
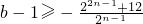 =
=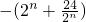 恒成立.
恒成立.点评:本题考查数列与函数的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目