题目内容
据统计,从5月1日到5月7号参观上海世博会的人数如表所示:| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数(万) | 21 | 23 | 13 | 15 | 9 | 12 | 14 |
(Ⅰ)把这7天的参观人数看成一个总体,求该总体的平均数(精确到0.1)
(Ⅱ)用简单随机抽样方法从非指定参观日中抽取2天,它们的参观人数组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过2万的概率.
【答案】分析:(1)根据所给的7个数据,利用求平均数的公式,求出这组数据的平均数.
(II)本题是一个古典概型,试验发生包含的事件是从非指定参观日中抽取2天可能的基本事件可以通过列举得到共有6种结果,满足条件的事件是样本平均数与总体平均数之差的绝对值不超过2万,列举出来,得到概率.
解答:解:(Ⅰ)总体平均数为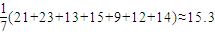
(Ⅱ)由题意知本题是一个古典概型,
设A表示事件“样本平均数与总体平均数之差的绝对值不超过2万”
试验发生包含的事件是从非指定参观日中抽取2天可能的基本事件有:(15,9),
(15,12),(15,14),(9,12),(9,14),(12,14)共有6个结果,
满足条件的事件A包含的基本事件有:(15,12),(15,14),共2个.
∴根据古典概型概率公式得到
点评:本题考查一组数据的平均数,考查古典概型及其概率公式,考查利用列举法求出事件数,在古典概型中利用列举法是最好的一种方法.
(II)本题是一个古典概型,试验发生包含的事件是从非指定参观日中抽取2天可能的基本事件可以通过列举得到共有6种结果,满足条件的事件是样本平均数与总体平均数之差的绝对值不超过2万,列举出来,得到概率.
解答:解:(Ⅰ)总体平均数为
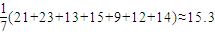
(Ⅱ)由题意知本题是一个古典概型,
设A表示事件“样本平均数与总体平均数之差的绝对值不超过2万”
试验发生包含的事件是从非指定参观日中抽取2天可能的基本事件有:(15,9),
(15,12),(15,14),(9,12),(9,14),(12,14)共有6个结果,
满足条件的事件A包含的基本事件有:(15,12),(15,14),共2个.
∴根据古典概型概率公式得到

点评:本题考查一组数据的平均数,考查古典概型及其概率公式,考查利用列举法求出事件数,在古典概型中利用列举法是最好的一种方法.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
据统计,从5月1日到5月7号参观上海世博会的人数如表所示:
其中,5月1日到5月3日为指定参观日,5月4日到5月7日为非指定参观日.
(Ⅰ)把这7天的参观人数看成一个总体,求该总体的平均数(精确到0.1)
(Ⅱ)用简单随机抽样方法从非指定参观日中抽取2天,它们的参观人数组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过2万的概率.
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数(万) | 21 | 23 | 13 | 15 | 9 | 12 | 14 |
(Ⅰ)把这7天的参观人数看成一个总体,求该总体的平均数(精确到0.1)
(Ⅱ)用简单随机抽样方法从非指定参观日中抽取2天,它们的参观人数组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过2万的概率.
据统计,从5月1日到5月7号参观上海世博会的人数如表所示:
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数(万) | 21 | 23 | 13 | 15 | 9 | 12 | 14 |
(Ⅰ)把这7天的参观人数看成一个总体,求该总体的平均数(精确到0.1)
(Ⅱ)用简单随机抽样方法从非指定参观日中抽取2天,它们的参观人数组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过2万的概率.