题目内容
已知点F是抛物线C:y2=4x的焦点,过点F且斜率为
的直线交抛物线C于A、B两点,设|FA|>|FB|,则
的值等于( )
| 3 |
| |FA| |
| |FB| |
分析:由点F是抛物线C:y2=4x的焦点,知F(1,0),所以过点F且斜率为
的直线方程为:y=
(x-1),联立方程组
,得3(x-1)2=4x,解得x1=3,x2=
,由|FA|>|FB|,能求出
.
| 3 |
| 3 |
|
| 1 |
| 3 |
| |FA| |
| |FB| |
解答:解:∵点F是抛物线C:y2=4x的焦点,∴F(1,0),
∴过点F且斜率为
的直线方程为:y=
(x-1),
联立方程组
,得3(x-1)2=4x,
解得x1=3,x2=
,
∵|FA|>|FB|,
∴
=
=
=3.
故选B.
∴过点F且斜率为
| 3 |
| 3 |
联立方程组
|
解得x1=3,x2=
| 1 |
| 3 |
∵|FA|>|FB|,
∴
| |FA| |
| |FB| |
| x1-1 |
| 1-x2 |
| 2 | ||
|
故选B.
点评:考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
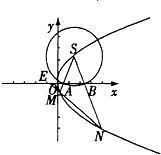 已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=
已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|= 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= .
.
 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点; |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值. 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= .
. 
 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点; |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值. 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= 。
。 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;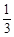 |NE|,求cos∠MSN的值。
|NE|,求cos∠MSN的值。