题目内容
已知双曲线x2-y2=2，过定点P（2，0）作直线l与双曲线有且只有一个交点，则这样的直线l的条数为（ ）
分析：设直线l的方程为y=k（x-2），与双曲线的方程联立转化为分类讨论其解的情况，即可得出．
解答：解：如图所示．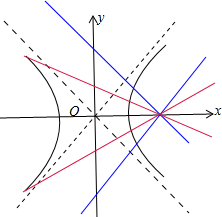
由题意可知直线l的斜率存在，设直线l的方程为y=k（x-2），
联立
，化为（1-k2）x2+4k2x-4k2-2=0，
①当1-k2=0时，解得k=±1，得到直线l：y=±（x-2），分别与渐近线y=±x平行，因此与双曲线只有一个交点，满足题意；
②当1-k2≠0时，由△=16k4-4（1-k2）（-4k2-2）=0，解得k=±
．
得到直线l：y=±
(x-2)，此时直线l分别与双曲线的作支相切，故只有一个交点．
综上可知：过定点P（2，0）作直线l与双曲线有且只有一个交点的这样的直线l只有4条．
故选D．
由题意可知直线l的斜率存在，设直线l的方程为y=k（x-2），
联立
|
①当1-k2=0时，解得k=±1，得到直线l：y=±（x-2），分别与渐近线y=±x平行，因此与双曲线只有一个交点，满足题意；
②当1-k2≠0时，由△=16k4-4（1-k2）（-4k2-2）=0，解得k=±
| ||
| 3 |
得到直线l：y=±
| ||
| 3 |
综上可知：过定点P（2，0）作直线l与双曲线有且只有一个交点的这样的直线l只有4条．
故选D．
点评：本题考查了直线与双曲线的位置关系转化为方程联立利用△分类讨论等基础知识与基本技能方法，属于难题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
已知双曲线x2-y2=a2（a＞0）的左、右顶点分别为A、B，双曲线在第一象限的图象上有一点P，∠PAB=α，∠PBA=β，∠APB=γ，则（ ）
| A、tanα+tanβ+tanγ=0 | B、tanα+tanβ-tanγ=0 | C、tanα+tanβ+2tanγ=0 | D、tanα+tanβ-2tanγ=0 |