题目内容
已知直线l1:ax-y-b=0; l2:bx-y+a=0,(a≠b,ab≠0),则它们的图象为
- A.
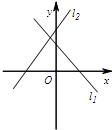
- B.
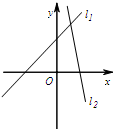
- C.
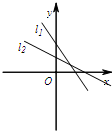
- D.
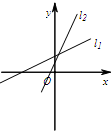
B
分析:结合图象,根据两直线y1=ax-b和y2=bx+a分别经过第几象限,确定对应的一次函数的系数和常数项,即可判断对错.
解答:对于A,由y1=ax-b经过第一,二,四象限知a<0,b<0,由y2=bx+a过第一,二,三象限知b>0,a>0,故A错误;
对于B,由y1=ax-b经过第一,二,三象限知a>0,b<0,由y2=bx+a过第一,二,四象限知b<0,a>0,故B正确;
对于C,由y1=ax-b经过第一,二,四象限,可知a<0,b<0,由y2=bx+a过第一,二,四象限知b<0,a>0,故C错误;
对于D,由y1=ax-b经过第一,二,三象限,可知a>0,b<0,由y2=bx+a过第一,二,三象限知b>0,a>0,故D错误;
故选B.
点评:本题的考点是确定直线为主的几何要素,考查直线的斜率和截距的问题,属于基础题,关键是掌握一次函数图象的单调性与系数的关系
分析:结合图象,根据两直线y1=ax-b和y2=bx+a分别经过第几象限,确定对应的一次函数的系数和常数项,即可判断对错.
解答:对于A,由y1=ax-b经过第一,二,四象限知a<0,b<0,由y2=bx+a过第一,二,三象限知b>0,a>0,故A错误;
对于B,由y1=ax-b经过第一,二,三象限知a>0,b<0,由y2=bx+a过第一,二,四象限知b<0,a>0,故B正确;
对于C,由y1=ax-b经过第一,二,四象限,可知a<0,b<0,由y2=bx+a过第一,二,四象限知b<0,a>0,故C错误;
对于D,由y1=ax-b经过第一,二,三象限,可知a>0,b<0,由y2=bx+a过第一,二,三象限知b>0,a>0,故D错误;
故选B.
点评:本题的考点是确定直线为主的几何要素,考查直线的斜率和截距的问题,属于基础题,关键是掌握一次函数图象的单调性与系数的关系

练习册系列答案
相关题目