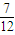题目内容
连续投掷两次骰子得到的点数分别为m、n,作向量a=(m,n).则向量a与向量b=(1,-1)的夹角成为直角三角形内角的概率是( )
分析:由题意知本题是一个古典概型,根据分步计数原理可以得到试验发生包含的所有事件数,满足条件的事件数要通过列举得到,题目大部分内容考查的是向量的问题,这是一个综合题.
解答:解:由题意知本题是一个古典概型,
试验发生包含的所有事件数6×6,
∵m>0,n>0,
∴
=(m,n)与
=(1,-1)不可能同向.
∴夹角θ≠0.
∵θ∈(0,
】
•
≥0,∴m-n≥0,
即m≥n.
当m=6时,n=6,5,4,3,2,1;
当m=5时,n=5,4,3,2,1;
当m=4时,n=4,3,2,1;
当m=3时,n=3,2,1;
当m=2时,n=2,1;
当m=1时,n=1.
∴满足条件的事件数6+5+4+3+2+1
∴概率P=
=
.
故选A.
试验发生包含的所有事件数6×6,
∵m>0,n>0,
∴
| a |
| b |
∴夹角θ≠0.
∵θ∈(0,
| π |
| 2 |
| a |
| b |
即m≥n.
当m=6时,n=6,5,4,3,2,1;
当m=5时,n=5,4,3,2,1;
当m=4时,n=4,3,2,1;
当m=3时,n=3,2,1;
当m=2时,n=2,1;
当m=1时,n=1.
∴满足条件的事件数6+5+4+3+2+1
∴概率P=
| 6+5+4+3+2+1 |
| 6×6 |
| 7 |
| 12 |
故选A.
点评:向量知识,向量观点在数学.物理等学科的很多分支有着广泛的应用,而它具有代数形式和几何形式的“双重身份”能融数形于一体,能与中学数学教学内容的许多主干知识综合,形成知识交汇点.

练习册系列答案
相关题目
 ,向量
,向量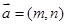 与向量
与向量 的夹角记为
的夹角记为 ,则
,则 的概率为
的概率为  B.
B. C.
C. D.
D.
 与向量
与向量 的夹角记为α,则α
的夹角记为α,则α 的概率为( )
的概率为( )