题目内容
一个袋中装有5个形状大小完全相同的球,其中有2个红球,3个白球.
(1)从袋中随机取两个球,求取出的两个球颜色不同的概率;
(2)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,求两次取出的球中至少有一个红球的概率.
(1)从袋中随机取两个球,求取出的两个球颜色不同的概率;
(2)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,求两次取出的球中至少有一个红球的概率.
(1) 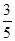 (2)
(2) 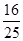
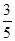 (2)
(2) 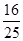
试题分析:(1)此概率问题属古典概型,借助字母,列出从装有5个球的袋子中随机取出两个球的十种情况,由于是随机取的,每个结果出现的可能性是相等的,符合古典概型的特征,然后设事件
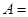 “取出的两个球颜色不同”,计算出事件A所包含的基本事件的个数,可由
“取出的两个球颜色不同”,计算出事件A所包含的基本事件的个数,可由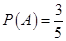
(2)与(1)不同,从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,一共有25个结果,由于是随机取的,每个结果出现的可能性是相等的,根据所罗列出的25种结果,可知至少有一个红球的结果有16个,由古典概型的概率公式可得所求概率.
试题解析:
解:(1)2个红球记为
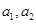 ,3个白球记为
,3个白球记为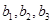
从袋中随机取两个球,其中一切可能的结果组成的基本事件有:
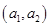 ,
,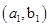 ,
,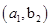 ,
,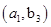 ,
,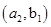 ,
,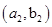 ,
, ,
,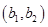 ,
,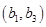 ,
,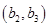 共10个 2分
共10个 2分设事件
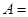 “取出的两个球颜色不同”
“取出的两个球颜色不同”中的基本事件有:
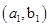 ,
,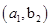 ,
,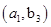
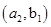 ,
,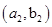 ,
, 共6个 4分
共6个 4分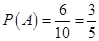 6分
6分(2)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,其一切可能的结果组成的基本事件有:
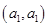 ,
,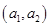 ,
,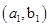 ,
,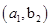 ,
,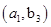 ,
,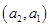 ,
,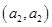 ,
,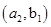 ,
,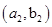 ,
, ,
,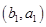 ,
,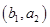 ,
,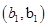 ,
,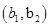 ,
,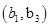 ,
,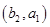 ,
,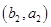 ,
,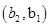 ,
,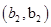 ,
,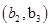 ,
,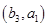 ,
,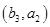 ,
,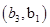 ,
,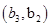 ,
,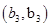 共25个. 8分
共25个. 8分设事件
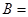 “两次取出的球中至少有一个红球”
“两次取出的球中至少有一个红球”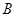 中的基本事件有:
中的基本事件有: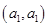 ,
,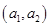 ,
,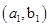 ,
,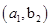 ,
,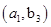 ,
,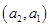 ,
,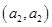 ,
,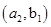 ,
,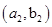 ,
, ,
,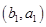 ,
,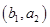 ,
,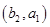 ,
,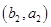 ,
,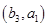 ,
,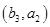 共16个. 10分
共16个. 10分所以
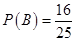 . 12分
. 12分
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 位学生,每次活动均需该系
位学生,每次活动均需该系 位学生参加(
位学生参加(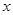
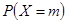 取得最大值的整数
取得最大值的整数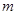 。
。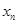 表示编号为
表示编号为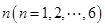 的同学的体重,且前5位同学的体重如下:
的同学的体重,且前5位同学的体重如下: 及这6位同学体重的标准差
及这6位同学体重的标准差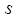 ;
; 中的概率.
中的概率.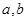 .
.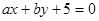 与圆
与圆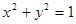 相切的概率;
相切的概率;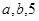 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.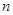 个黑球(
个黑球(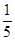 ,求
,求 ,则从袋中一次随机摸两个球,得到一个白色乒乓球和一个黄色乒乓球的概率是.
,则从袋中一次随机摸两个球,得到一个白色乒乓球和一个黄色乒乓球的概率是.