题目内容
定义Mxn=x(x+1)(x+2)…(x+n-1),其中x∈R,n∈N*,例如M-44=(-4)(-3)(-2)(-1)=24,则函数f(x)=Mx-10042009的奇偶性为
奇函数
奇函数
.分析:由已知定义可求出函数f(x)的关系式,根据函数的奇偶性的定义寻找f(-x)与f(x)的关系.可判断
解答:解:由题意可得,f(x)=
=(x-1004)(x-1003)…(x+1003)(x+1004)
=(x2-10042)(x2-10032)…(x2-1)x
从而f(-x)=(x2-10042)(x2-10032)…(x2-1)(-x)=-f(x),
又因为该函数的定义域是R,故该函数是奇函数
故答案为:奇函数
| M | 2009 x-1004 |
=(x2-10042)(x2-10032)…(x2-1)x
从而f(-x)=(x2-10042)(x2-10032)…(x2-1)(-x)=-f(x),
又因为该函数的定义域是R,故该函数是奇函数
故答案为:奇函数
点评:题是新定义型问题,考查学生对新定义函数的认识和理解能力,也可以类比学过的排列数公式理解该函数.考查学生奇偶性的判断和化归能力,属于函数性质的应用问题.

练习册系列答案
相关题目
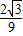 ;②f (x)为奇函数;③f(x)的图象不具备对称性;④f (x)在
;②f (x)为奇函数;③f(x)的图象不具备对称性;④f (x)在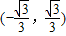 上是减函数,
上是减函数,