题目内容
若对任意的自然数n,Sn=| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n×(n+1) |
| 10 |
| 11 |
分析:利用裂项求和可先求Sn=
,然后由
=
进而可求n的值
| n |
| n+1 |
| n |
| n+1 |
| 10 |
| 11 |
解答:解:Sn=
+
+…+
=1-
+
-
+…+
-
=1-
=
=
所以,n=10
故答案为:10
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| n(n+1) |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
| n |
| n+1 |
| 10 |
| 11 |
所以,n=10
故答案为:10
点评:本题主要考查数列求和的裂项法.考查学生的运算能力.属于基本方法的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则n=________.
,则n=________.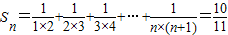 ,则n= .
,则n= . ,则n=( )。
,则n=( )。