题目内容
已知数列{an}为等差数列,公差d≠0,{an}的部分项组成下列数列:ak1,ak2,…,akn,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.分析:运用等差(比)数列的定义分别求得akn,然后列方程求得kn.
解答:解:设{an}的首项为a1,∵ak1,ak2,ak3成等比数列,
∴(a1+4d)2=a1(a1+16d).
得a1=2d,q=
=3.
∵akn=a1+(kn-1)d,又akn=a1•3n-1,
∴kn=2•3n-1-1.
∴k1+k2+…+kn=2(1+3+…+3n-1)-n
=2×
-n=3n-n-1.
∴(a1+4d)2=a1(a1+16d).
得a1=2d,q=
| ak2 |
| ak1 |
∵akn=a1+(kn-1)d,又akn=a1•3n-1,
∴kn=2•3n-1-1.
∴k1+k2+…+kn=2(1+3+…+3n-1)-n
=2×
| 1-3n |
| 1-3 |
点评:运用等差(比)数列的定义转化为关于kn的方程是解题的关键,转化时要注意:akn是等差数列中的第kn项,而是等比数列中的第n项.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

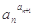 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4