题目内容
以下正确命题的序号为
①命题“存在x0∈R,2x0≤0”的否定是:“不存在x0∈R,2x0>0
②函数f(x)=x
-(
)x的零点在区间(
,
)内;
③若函数f(x)满足f(1)=1且f(x+1)=2f(x),则f(1)+f(2)+…+f(10)=1023;
④若m≥-1,则函数的值域为y=log
(x2-2x-m)的值域为R.
②③④
②③④
.①命题“存在x0∈R,2x0≤0”的否定是:“不存在x0∈R,2x0>0
②函数f(x)=x
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
③若函数f(x)满足f(1)=1且f(x+1)=2f(x),则f(1)+f(2)+…+f(10)=1023;
④若m≥-1,则函数的值域为y=log
| 1 |
| 2 |
分析:根据命题的否定可以得到①不正确;
根据函数零点的判定定理可得②正确.
根据等比数列的前n项和公式可得③正确.
根据对数的真数可取遍所有的正实数,可得此对数函数的值域为R,故④正确.
根据函数零点的判定定理可得②正确.
根据等比数列的前n项和公式可得③正确.
根据对数的真数可取遍所有的正实数,可得此对数函数的值域为R,故④正确.
解答:解:①命题“存在x0∈R,2x0≤0”的否定是:“任意x0∈R,2x0>0,故①错误;
②∵f(x)=x
-(
)x,
∴f(
)=(
)
-(
)
<0,f(
)=(
)
-(
)
>0,
∴f(x)的零点在区间(
,
)内,故②正确;
③∵函数f(x)满足f(1)=1且f(x+1)=2f(x),
∴f(2)=2×1=2,f(3)=2×2=4,f(4)=2×4=8,f(5)=2×8=16,
f(6)=2×16=32,f(7)=2×32=64,f(8)=2×64=128,
f(9)=2×128=256,f(10)=2×256=512,
∴f(1)+f(2)+…+f(10)=1023,故③正确;
④当 m≥-1,函数y=log
(x2-2x-m)的真数为 x2-2x-m,
判别式△=4+4m≥0,故真数可取遍所有的正实数,
故函数y=log
(x2-2x-m)的值域为R,故④正确.
故答案为:②③④.
②∵f(x)=x
| 1 |
| 3 |
| 1 |
| 4 |
∴f(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
∴f(x)的零点在区间(
| 1 |
| 4 |
| 1 |
| 3 |
③∵函数f(x)满足f(1)=1且f(x+1)=2f(x),
∴f(2)=2×1=2,f(3)=2×2=4,f(4)=2×4=8,f(5)=2×8=16,
f(6)=2×16=32,f(7)=2×32=64,f(8)=2×64=128,
f(9)=2×128=256,f(10)=2×256=512,
∴f(1)+f(2)+…+f(10)=1023,故③正确;
④当 m≥-1,函数y=log
| 1 |
| 2 |
判别式△=4+4m≥0,故真数可取遍所有的正实数,
故函数y=log
| 1 |
| 2 |
故答案为:②③④.
点评:本题主要考查命题的真假的判断,通过举反例来说明某个命题不正确,是一种简单有效的方法,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
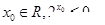 ”的否定是:“不存在
”的否定是:“不存在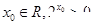 ”;
”; 的零点在区间
的零点在区间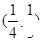 内;
内;  满足
满足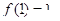 且
且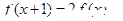 ,则
,则 =1023;
=1023; 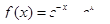 切线斜率的最大值是2.
切线斜率的最大值是2. ”的否定是:“不存在
”的否定是:“不存在
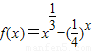 的零点在区间(
的零点在区间(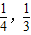 )内;
)内;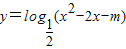 的值域为R.
的值域为R.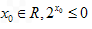 的否定是:不存在
的否定是:不存在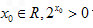 ”;
”; 的零点在区间
的零点在区间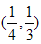 内;
内; 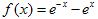 切线斜率的最大值是2.
切线斜率的最大值是2.