题目内容
如图,在?ABCD中,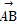 =a,
=a,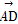 =b,
=b,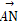 =3
=3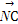 ,M是BC的中点,则
,M是BC的中点,则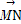 = (用a,b表示).
= (用a,b表示).
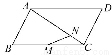
-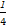 a+
a+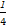 b
b
【解析】由题意知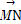 =
=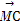 +
+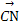
=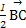 +
+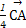 =
=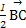 -
-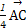
=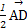 -
-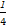 (
(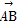 +
+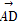 )
)
=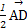 -
-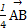 -
-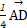 =-
=-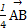 +
+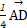
=-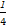 a+
a+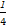 b.
b.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
题目内容
如图,在?ABCD中,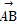 =a,
=a,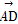 =b,
=b,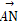 =3
=3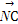 ,M是BC的中点,则
,M是BC的中点,则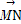 = (用a,b表示).
= (用a,b表示).

-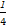 a+
a+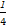 b
b
【解析】由题意知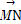 =
=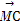 +
+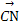
=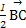 +
+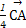 =
=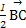 -
-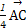
=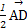 -
-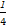 (
(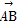 +
+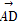 )
)
=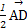 -
-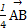 -
-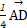 =-
=-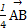 +
+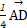
=-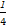 a+
a+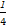 b.
b.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案