题目内容
(1)若关于x的不等式|x-1|+|x+m|>3的解集为R,则实数m的取值范围是 .(2)已知⊙O的割线PAB交⊙于A,B两点,割线PCD经过圆心,若PA=3,AB=4,PO=5,则⊙O的半径为 .
(3)过点
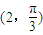 且平行于极轴的直线的极坐标方程为 .
且平行于极轴的直线的极坐标方程为 .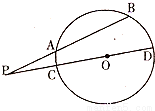
【答案】分析:(1)利用绝对值的几何意义可得,若使不等式|x-1|+|x+m|>3的解集为R,只需数轴上点A(其坐标为1)与点B(其坐标为-m)之间的距离大于3即可.
(2)设⊙O的半径为R,由于PA=3,AB=4,PO=5,由PA•PB=PC•PD即可求得⊙O的半径;
(3)由题意可得,过点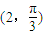 且平行于极轴的直线与极轴之间的距离为
且平行于极轴的直线与极轴之间的距离为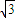 ,从而可得过点
,从而可得过点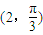 且平行于极轴的直线的极坐标方程.
且平行于极轴的直线的极坐标方程.
解答:解:(1)设数轴上点A的坐标为1,点B的坐标为-m,|AB|=|1+m|,
∵不等式|x-1|+|x+m|>3的解集为R,
∴|1+m|>3,
∴m<-4或m>2;
故答案为:(-∞,-4)∪(2,+∞);
(2)设⊙O的半径为R,∵PA=3,AB=4,PO=5,
∴PC=PO-R=5-R,PD=PO+R=5+R,
由割线定理得,PA•PB=PC•PD,即3×(3+4)=(5-R)(5+R),
∴R2=4,又R>0,
∴R=2.
故答案为:2;
(3)∵2sin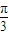 =
=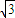 ,
,
∴过点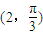 且平行于极轴的直线与极轴之间的距离为
且平行于极轴的直线与极轴之间的距离为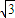 ,
,
∴过点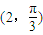 且平行于极轴的直线的极坐标方程为ρsinθ=
且平行于极轴的直线的极坐标方程为ρsinθ=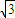 .
.
故答案为:ρsinθ=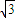 .
.
点评:本题(1)考查绝对值不等式,理解绝对值的几何意义是关键;(2)考查割线长定理的应用,⊙O的半径为R,PA•PB=PC•PD是求求值的关键;(3)考查简单曲线的极坐标方程,明确“过点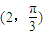 且平行于极轴的直线与极轴之间的距离为
且平行于极轴的直线与极轴之间的距离为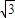 ”是关键,属于中档题.
”是关键,属于中档题.
(2)设⊙O的半径为R,由于PA=3,AB=4,PO=5,由PA•PB=PC•PD即可求得⊙O的半径;
(3)由题意可得,过点
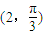 且平行于极轴的直线与极轴之间的距离为
且平行于极轴的直线与极轴之间的距离为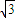 ,从而可得过点
,从而可得过点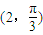 且平行于极轴的直线的极坐标方程.
且平行于极轴的直线的极坐标方程.解答:解:(1)设数轴上点A的坐标为1,点B的坐标为-m,|AB|=|1+m|,
∵不等式|x-1|+|x+m|>3的解集为R,
∴|1+m|>3,
∴m<-4或m>2;
故答案为:(-∞,-4)∪(2,+∞);
(2)设⊙O的半径为R,∵PA=3,AB=4,PO=5,
∴PC=PO-R=5-R,PD=PO+R=5+R,
由割线定理得,PA•PB=PC•PD,即3×(3+4)=(5-R)(5+R),
∴R2=4,又R>0,
∴R=2.
故答案为:2;
(3)∵2sin
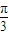 =
=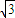 ,
,∴过点
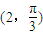 且平行于极轴的直线与极轴之间的距离为
且平行于极轴的直线与极轴之间的距离为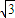 ,
,∴过点
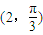 且平行于极轴的直线的极坐标方程为ρsinθ=
且平行于极轴的直线的极坐标方程为ρsinθ=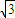 .
.故答案为:ρsinθ=
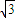 .
.点评:本题(1)考查绝对值不等式,理解绝对值的几何意义是关键;(2)考查割线长定理的应用,⊙O的半径为R,PA•PB=PC•PD是求求值的关键;(3)考查简单曲线的极坐标方程,明确“过点
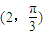 且平行于极轴的直线与极轴之间的距离为
且平行于极轴的直线与极轴之间的距离为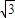 ”是关键,属于中档题.
”是关键,属于中档题. 
练习册系列答案
相关题目