题目内容
(本小题满分12分)己知函数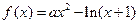 ,
,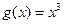
(1)求函数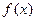 的单调区间;
的单调区间;
(2)当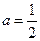 时,证明:对
时,证明:对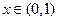 时,不等式
时,不等式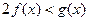 成立;
成立;
(3)当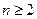 ,
,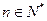 时,证明:
时,证明: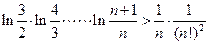 .
.
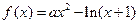 ,
,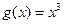
(1)求函数
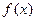 的单调区间;
的单调区间;(2)当
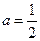 时,证明:对
时,证明:对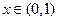 时,不等式
时,不等式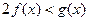 成立;
成立;(3)当
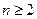 ,
,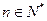 时,证明:
时,证明: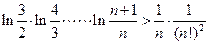 .
.略
(1)
 , ……1分
, ……1分 
① 时,
时, ,单调减区间
,单调减区间 ;……1分
;……1分
② 时,
时, ,单调减区间
,单调减区间 ;增区间
;增区间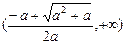 ……1分
……1分
③ 时,
时, ,单调减区间
,单调减区间 ,
, ;增区间
;增区间 ……2分
……2分
(2)设 ,
, ,……2分
,……2分
所以 ,即
,即 ……1分
……1分
(3)由(2)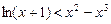 ,令
,令 ,则
,则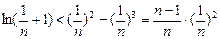 ,…2分
,…2分
同理 ,……,……
,……,……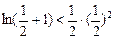 ,累乘
,累乘 即证 ……2分
即证 ……2分

 , ……1分
, ……1分 
①
 时,
时, ,单调减区间
,单调减区间 ;……1分
;……1分②
 时,
时, ,单调减区间
,单调减区间 ;增区间
;增区间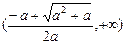 ……1分
……1分③
 时,
时, ,单调减区间
,单调减区间 ,
, ;增区间
;增区间 ……2分
……2分(2)设
 ,
, ,……2分
,……2分所以
 ,即
,即 ……1分
……1分(3)由(2)
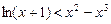 ,令
,令 ,则
,则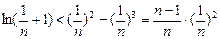 ,…2分
,…2分同理
 ,……,……
,……,……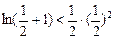 ,累乘
,累乘 即证 ……2分
即证 ……2分
练习册系列答案
相关题目
 在
在 处取得极值5,
处取得极值5, 的值;
的值; 上的最大值
上的最大值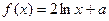 (
(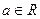 )与函数
)与函数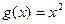 ,
,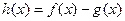 的单调区间;
的单调区间;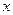 的方程
的方程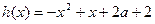 在区间[1,3]内恰有两个相异的实根,求实数
在区间[1,3]内恰有两个相异的实根,求实数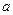 的取值范围.
的取值范围.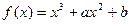 的图象在点
的图象在点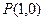 处的切线与直线
处的切线与直线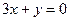 平行.
平行.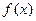 的解析式;
的解析式;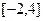 上的最小值和最大值.
上的最小值和最大值.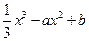 在x=-2处有极值.
在x=-2处有极值.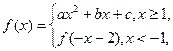 其图像在点
其图像在点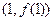 处的切线方程为
处的切线方程为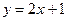 ,则它在点
,则它在点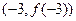 处的切线方程为( )
处的切线方程为( )


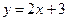


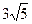
 作曲线
作曲线 的两条切线
的两条切线 设它们的夹角为
设它们的夹角为 ,则
,则 的值为( )
的值为( )
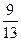


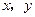 满足
满足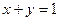 ,,则
,,则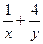 的最小值为______________
的最小值为______________