题目内容
已知椭圆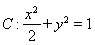 的左、右焦点分别为
的左、右焦点分别为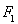 、
、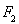 ,
,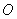 为原点.
为原点.
(1)如图1,点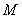 为椭圆
为椭圆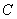 上的一点,
上的一点,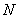 是
是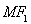 的中点,且
的中点,且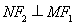 ,求点
,求点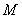 到
到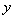 轴的距离;
轴的距离;

(2)如图2,直线 与椭圆
与椭圆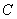 相交于
相交于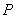 、
、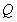 两点,若在椭圆
两点,若在椭圆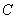 上存在点
上存在点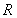 ,使四边形
,使四边形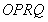 为平行四边形,求
为平行四边形,求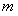 的取值范围.
的取值范围.

【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先设点 的坐标,并利用点
的坐标,并利用点 的坐标来表示点
的坐标来表示点 的坐标,利用
的坐标,利用 以及点
以及点 在椭圆
在椭圆 上列方程组求解点
上列方程组求解点 的坐标,从而求出点
的坐标,从而求出点 到
到 轴的距离;(2)先设点
轴的距离;(2)先设点 、
、 ,利用
,利用 为平行四边形,得到
为平行四边形,得到 ,将直线方程与椭圆方程联立,结合韦达定理与点
,将直线方程与椭圆方程联立,结合韦达定理与点 在椭圆上这一条件,列相应等式求出实数
在椭圆上这一条件,列相应等式求出实数 的取值范围.
的取值范围.
试题解析:(1)由已知得 、
、 ,
,
设 ,则
,则 的中点为
的中点为 ,
,
 ,
, ,即
,即 ,
,
整理得 ,①,又有
,①,又有 ,②
,②
由①②联立解得 或
或 (舍)
(舍)
 点
点 到
到 轴的距离为
轴的距离为 ;
;
(2)设 ,
, ,
, ,
,
 四边形
四边形 是平行四边形
是平行四边形
 线段
线段 的中点即为线段
的中点即为线段 的中点,即
的中点,即 ,
, ,
,
 点
点 在椭圆上,
在椭圆上, ,
,
即 ,
,
化简得 ,
,
由 得
得 ,
,
由 得
得 ,④
,④
且 ,代入③式得
,代入③式得 ,
,
整理得 代入④式得
代入④式得 ,又
,又 ,
, 或
或 ,
,
 的取值范围是
的取值范围是 .
.
考点:1.直线与椭圆的位置关系;2.韦达定理

练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线