题目内容
已知△ABC的周长为 +1,且sinA+sinB=
+1,且sinA+sinB= sinC,△ABC的面积为
sinC,△ABC的面积为 sinC.
sinC.
(1)求边AB的长;
(2)求tan(A+B)的值.
解:(1)因为△ABC的周长为 ,所以
,所以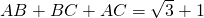 .----------(1分)
.----------(1分)
又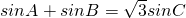 ,由正弦定理得
,由正弦定理得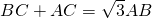 .--------------(3分)
.--------------(3分)
两式相减,得AB=1.------------(4分)
(2)由于△ABC的面积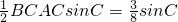 ,得
,得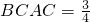 ,-----(6分)
,-----(6分)
由余弦定理得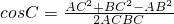 ------------(8分)
------------(8分)
= ,---------(10分)
,---------(10分)
又0°<C<180°,所以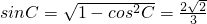 .------------(12分)
.------------(12分)
故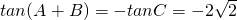 .----------(14分)
.----------(14分)
分析:(1)由条件得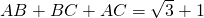 ,再由正弦定理得
,再由正弦定理得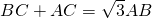 ,两式相减求得AB的值.
,两式相减求得AB的值.
(2)由△ABC的面积为 sinC求得
sinC求得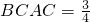 ,由余弦定理求得cosC=
,由余弦定理求得cosC= ,可得sinC=
,可得sinC= ,求出tanC的值,利用诱导公式求得tan(A+B)的值.
,求出tanC的值,利用诱导公式求得tan(A+B)的值.
点评:本题主要考查正弦定理、余弦定理以及诱导公式,已知三角函数值求角的大小,属于中档题.
 ,所以
,所以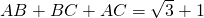 .----------(1分)
.----------(1分)又
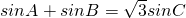 ,由正弦定理得
,由正弦定理得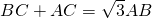 .--------------(3分)
.--------------(3分)两式相减,得AB=1.------------(4分)
(2)由于△ABC的面积
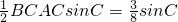 ,得
,得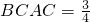 ,-----(6分)
,-----(6分)由余弦定理得
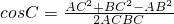 ------------(8分)
------------(8分)=
 ,---------(10分)
,---------(10分)又0°<C<180°,所以
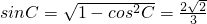 .------------(12分)
.------------(12分)故
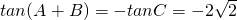 .----------(14分)
.----------(14分)分析:(1)由条件得
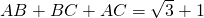 ,再由正弦定理得
,再由正弦定理得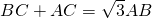 ,两式相减求得AB的值.
,两式相减求得AB的值.(2)由△ABC的面积为
 sinC求得
sinC求得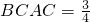 ,由余弦定理求得cosC=
,由余弦定理求得cosC= ,可得sinC=
,可得sinC= ,求出tanC的值,利用诱导公式求得tan(A+B)的值.
,求出tanC的值,利用诱导公式求得tan(A+B)的值.点评:本题主要考查正弦定理、余弦定理以及诱导公式,已知三角函数值求角的大小,属于中档题.

练习册系列答案
相关题目