题目内容
(满分12分)已知函数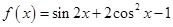 .
.
(1)求函数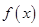 的最小正周期和最大值;
的最小正周期和最大值;
(2)求函数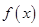 在区间
在区间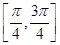 上的最大值与最小值.
上的最大值与最小值.
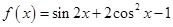 .
. (1)求函数
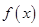 的最小正周期和最大值;
的最小正周期和最大值;(2)求函数
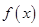 在区间
在区间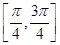 上的最大值与最小值.
上的最大值与最小值.(1) 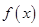 的最小正周期是
的最小正周期是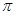 ;最大值是
;最大值是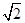 .
.
(2)函数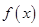 在区间
在区间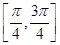 上的最大值是
上的最大值是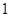 ,最小值是
,最小值是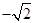 .
.
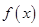 的最小正周期是
的最小正周期是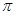 ;最大值是
;最大值是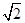 .
. (2)函数
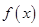 在区间
在区间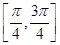 上的最大值是
上的最大值是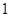 ,最小值是
,最小值是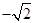 .
.试题分析:解:(Ⅰ)因为
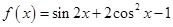 ,
,所以
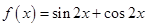
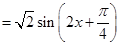 . ……………………….. 3分
. ……………………….. 3分所以其最小正周期为
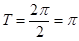 …………….. 5分
…………….. 5分又因为
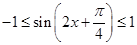 ,所以
,所以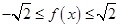 .
. 所以函数
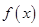 的最小正周期是
的最小正周期是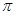 ;最大值是
;最大值是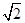 . …………………….. 7分
. …………………….. 7分(Ⅱ)由(Ⅰ)知
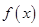
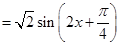 . 因为
. 因为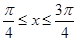 ,所以
,所以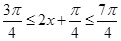 .
. 所以当
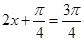 ,即
,即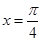 时,函数
时,函数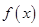 有最大值是
有最大值是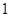 ;
;当
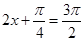 ,即
,即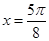 时,函数
时,函数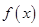 有最小值是
有最小值是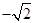 .
.所以函数
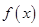 在区间
在区间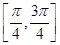 上的最大值是
上的最大值是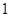 ,最小值是
,最小值是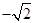 .……….. 12分
.……….. 12分点评:解决的关键是利用二倍角公式化为单一三角函数,然后求解函数的性质,属于基础题。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
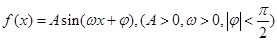 的最小正周期为
的最小正周期为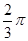 ,最小值为
,最小值为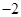 ,图象过点
,图象过点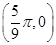 ,(1)求
,(1)求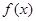 的解析式;(2)求满足
的解析式;(2)求满足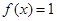 且
且
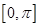 的
的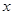 的集合.
的集合. ,则
,则 ( )
( ) ,
, ]上是减函数
]上是减函数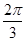 ,
, ]上是增函数
]上是增函数 ,
, ]上是增函数
]上是增函数 ,
, ]上是减函数
]上是减函数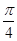 )的单调减区间为( )
)的单调减区间为( )



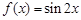 ,则
,则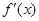 等于
等于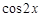
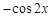

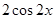
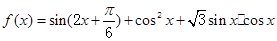 .
.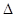 ABC的三个内角,若cosB=
ABC的三个内角,若cosB=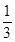 ,
,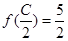 ,求sinA.
,求sinA.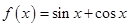 ,
,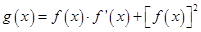
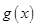 的周期和最大值
的周期和最大值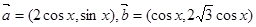 ,函数
,函数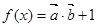 .
.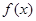 的单调递增区间;
的单调递增区间;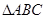 中,
中,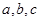 分别是角
分别是角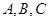 的对边,
的对边,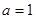 且
且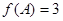 ,求
,求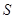 的最大值.
的最大值. 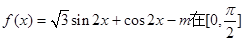 上有两个零点,则m的取值范围是
上有两个零点,则m的取值范围是