题目内容
(2013•黄浦区二模)如果函数y=|x|-2的图象与曲线C:x2+λy2=4恰好有两个不同的公共点,则实数λ的取值范围是( )
分析:利用绝对值的几何意义,由y=|x|-2可得,x≥0时,y=x-2;x<0时,y=-x-2,确定函数y=|x|-2的图象与方程x2+λy2=4的曲线必相交于(±2,0),为了使函数y=|x|-2的图象与方程x2+λy2=4的曲线恰好有两个不同的公共点,则两曲线无其它交点.y=x-2代入方程x2+λy2=4,整理可得(1+λ)x2-4λx+4λ-4=0,分类讨论,可得结论,根据对称性,同理可得x<0时的情形.
解答: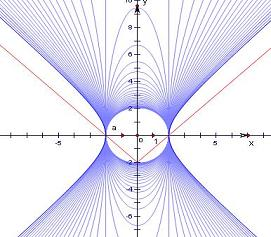 解:由y=|x|-2可得,x≥0时,y=x-2;x<0时,y=-x-2,
解:由y=|x|-2可得,x≥0时,y=x-2;x<0时,y=-x-2,
∴函数y=|x|-2的图象与方程x2+λy2=4的曲线必相交于(±2,0),如图.
所以为了使函数y=|x|-2的图象与方程x2+λy2=4的曲线恰好有两个不同的公共点,
则将y=x-2代入方程x2+λy2=4,
整理可得(1+λ)x2-4λx+4λ-4=0,
当λ=-1时,x=2满足题意,
由于△>0,2是方程的根,
∴
<0,即-1<λ<1时,方程两根异号,满足题意;
综上知,实数λ的取值范围是[-1,1).
故选A.
 解:由y=|x|-2可得,x≥0时,y=x-2;x<0时,y=-x-2,
解:由y=|x|-2可得,x≥0时,y=x-2;x<0时,y=-x-2,∴函数y=|x|-2的图象与方程x2+λy2=4的曲线必相交于(±2,0),如图.
所以为了使函数y=|x|-2的图象与方程x2+λy2=4的曲线恰好有两个不同的公共点,
则将y=x-2代入方程x2+λy2=4,
整理可得(1+λ)x2-4λx+4λ-4=0,
当λ=-1时,x=2满足题意,
由于△>0,2是方程的根,
∴
| 4(λ-1) |
| λ+1 |
综上知,实数λ的取值范围是[-1,1).
故选A.
点评:本题考查曲线的交点,考查学生分析解决问题的能力,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目