题目内容
设有两个命题:p:不等式(
)x+4>m>2x-x2对一切实数x恒成立;q:f(x)=-(9-2m)x是R上的减函数,如果p且q为假命题,则实数m的取值范围是
| 1 | 2 |
(-∞,1]∪[4,+∞)
(-∞,1]∪[4,+∞)
.分析:分别求出命题p,q成立的等价条件,先求出p且q为真命题的取值范围,然后确定实数m的取值范围.
解答:解:∵(
)x+4>4,2x-x2=-(x-1)2+1≤1,
要使不等式(
)x+4>m>2x-x2对一切实数x恒成立,
则1<m<4,即p:-1<m<4.
若方f(x)=-(9-2m)x是R上的减函数,
则9-2m>1,即2m<8,解得m<4,即q:m<4.
要使p且q为真,则
,解得-1<m<4.
所以当p且q为假命题时,解得m≥4或m≤-1.
即实数a的取值范围是(-∞,1]∪[4,+∞).
故答案为:(-∞,1]∪[4,+∞).
| 1 |
| 2 |
要使不等式(
| 1 |
| 2 |
则1<m<4,即p:-1<m<4.
若方f(x)=-(9-2m)x是R上的减函数,
则9-2m>1,即2m<8,解得m<4,即q:m<4.
要使p且q为真,则
|
所以当p且q为假命题时,解得m≥4或m≤-1.
即实数a的取值范围是(-∞,1]∪[4,+∞).
故答案为:(-∞,1]∪[4,+∞).
点评:本题主要考查复合命题与简单命题之间的关系,利用条件先求出p,q成立的等价条件是解决此类问题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
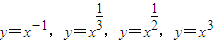 ,其中在R上是增函数的函数有3个.
,其中在R上是增函数的函数有3个.