题目内容
已知x是实数且x≠2，3．若S=min{
，
}，那么Smax=
．
| 1 |
| |x-2| |
| 1 |
| |x-3| |
2；
2；
，此时x=| 5 |
| 2 |
| 5 |
| 2 |
分析：先比较
，
的大小关系，再确定S的最大值．
| 1 |
| |x-2| |
| 1 |
| |x-3| |
解答：解：∵（x-2）2-（x-3）2=2x-5，
∴当2x-5＜0时，则x＜2.5（x≠2），
＞
当2x-5＜0时，则x＞2.5（x≠3），
＜
∴当x=2.5时，S取到最大值，Smax=2
故答案为：2，
∴当2x-5＜0时，则x＜2.5（x≠2），
| 1 |
| |x-2| |
| 1 |
| |x-3| |
当2x-5＜0时，则x＞2.5（x≠3），
| 1 |
| |x-2| |
| 1 |
| |x-3| |
∴当x=2.5时，S取到最大值，Smax=2
故答案为：2，
| 5 |
| 2 |
点评：本题考查带绝对值的函数，解题的关键是确定两个绝对值的大小关系，属于中档题．
练习册系列答案
相关题目
，那么Smax=________，此时x=________．
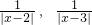，那么Smax=________，此时x=________．
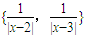，那么Smax= ，此时x= ．