题目内容
曲线y=ex在点(1,e)处的切线与x轴,直线x=1所围成的三角形面积为______.
依题意得y′=ex,
因此曲线y=ex在点A(1,e)处的切线的斜率等于e,
相应的切线方程是y-e=e(x-1),y=ex
当x=0时,y=0.即切线与坐标轴的交点为(0,0),
∴切线与x轴,直线x=1所围成的三角形面积为:
S=
×1×e=
e.
故答案为:
e.
因此曲线y=ex在点A(1,e)处的切线的斜率等于e,
相应的切线方程是y-e=e(x-1),y=ex
当x=0时,y=0.即切线与坐标轴的交点为(0,0),
∴切线与x轴,直线x=1所围成的三角形面积为:
S=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

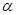 的顶点与原点重合,始边与x轴的非负半轴重合,终边过点
的顶点与原点重合,始边与x轴的非负半轴重合,终边过点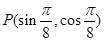 ,则sin(2
,则sin(2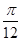 )=( )
)=( )


