题目内容
设函数
，集合M={x|f（x）＜0}，P={x|f'（x）＞0}，若M?P，则实数a的取值范围是（ ）A．（-∞，-1）
B．（0，1）
C．（1，+∞）
D．[1，+∞）
【答案】分析：结合题意，根据a的取值范围，分情况讨论，分别判断f（x）与f′（x）的符合，进一步得到答案．
解答：解：函数
，集合M={x|f（x）＜0}，f'（x）=
＞0，
若a＞1时，M={x|1＜x＜a}，P=R；
若a＜1时M={x|a＜x＜1}，，P=∅；
a=1时，M=∅；P={x|f'（x）＞0}={x|x≠1}，
故选C．
点评：本题有一定难度，要分情况讨论f（x）与f′（x）的符号，注意不要遗忘a=1的情况．
解答：解：函数
，集合M={x|f（x）＜0}，f'（x）=＞0，若a＞1时，M={x|1＜x＜a}，P=R；
若a＜1时M={x|a＜x＜1}，，P=∅；
a=1时，M=∅；P={x|f'（x）＞0}={x|x≠1}，
故选C．
点评：本题有一定难度，要分情况讨论f（x）与f′（x）的符号，注意不要遗忘a=1的情况．
练习册系列答案
高效智能课时作业系列答案
相关题目
，集合M={x|f（x）=0}={x1，x2，…，x7}⊆N*，设c1≥c2≥c3≥c4，则c1-c4=（ ）
，集合M={x|f（x）=0}={x1，x2，…，x7}⊆N*，设c1≥c2≥c3≥c4，则c1-c4=（ ）
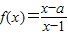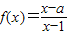，集合M={x|f（x）＜0}，P={x|f′（x）＞0}，若M⊆P，则实数a的取值范围是 ．
，集合M={x|f（x）＜0}，P={x|f'（x）＞0}，若M?P，则实数a的取值范围是（ ）
，集合M={x|f（x）＜0}，P={x|f'（x）＞0}，若M?P，则实数a的取值范围是（ ）