题目内容
已知椭圆C: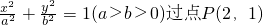 ,离心率
,离心率 ,则椭圆的方程是
,则椭圆的方程是
- A.
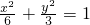
- B.

- C.
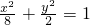
- D.
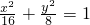
C
分析:先根据椭圆 求得焦点坐标,进而求得椭圆的半焦距c,根据椭圆的离心率
求得焦点坐标,进而求得椭圆的半焦距c,根据椭圆的离心率 求得a,b的关系式,再根据椭圆过点P(2,1)得到b与a的关系式,最后解方程组求得a,b即可.
求得a,b的关系式,再根据椭圆过点P(2,1)得到b与a的关系式,最后解方程组求得a,b即可.
解答:椭圆 ,
,
∴c=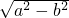 ,
,
∴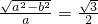 ①
①
∵椭圆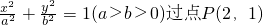
∴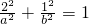 ②
②
解①②组成的方程组得:
∴b=2 ,a=
,a= ,
,
∴椭圆的标准方程为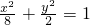
故选C.
点评:本题主要考查了椭圆的标准方程的问题.要熟练掌握椭圆方程中a,b和c的关系,求椭圆的方程时才能做到游刃有余.
分析:先根据椭圆
 求得焦点坐标,进而求得椭圆的半焦距c,根据椭圆的离心率
求得焦点坐标,进而求得椭圆的半焦距c,根据椭圆的离心率 求得a,b的关系式,再根据椭圆过点P(2,1)得到b与a的关系式,最后解方程组求得a,b即可.
求得a,b的关系式,再根据椭圆过点P(2,1)得到b与a的关系式,最后解方程组求得a,b即可.解答:椭圆
 ,
,∴c=
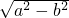 ,
,∴
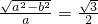 ①
①∵椭圆
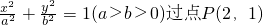
∴
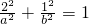 ②
②解①②组成的方程组得:
∴b=2
 ,a=
,a= ,
,∴椭圆的标准方程为
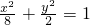
故选C.
点评:本题主要考查了椭圆的标准方程的问题.要熟练掌握椭圆方程中a,b和c的关系,求椭圆的方程时才能做到游刃有余.

练习册系列答案
相关题目
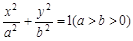 的离心率与等轴双曲线的离心率互为倒数,直线
的离心率与等轴双曲线的离心率互为倒数,直线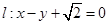 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。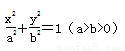 的离心率为
的离心率为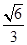 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为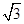 .
.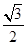 ,求△AOB面积的最大值.
,求△AOB面积的最大值. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线