题目内容
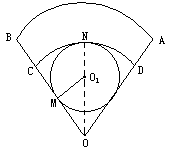
 如图,扇形AOB的圆心角为60°,半径为6cm,C,D分别是
如图,扇形AOB的圆心角为60°,半径为6cm,C,D分别是 | AB |
1
1
.分析:由题意可知C、D是弧AB的三等分点,通过平移可把阴影部分都集中到一个小扇形中,可发现阴影部分正好是扇形AOB的
,先求出扇形AOB的面积再求阴影部分的面积或者直接求圆心角是20度,半径是6的扇形的面积皆可.
| 1 |
| 3 |
解答:解:S扇形OAB=
=6π
S阴影=
S扇形OAB=
×6π=2π.
故答案为:2π.
| 60π•62 |
| 360 |
S阴影=
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:2π.
点评:通过平移的知识把小块的阴影部分集中成一个规则的图形--扇形,再求算扇形的面积即可.利用平移或割补把不规则图形变成规则图形求面积是常用的方法.

练习册系列答案
相关题目
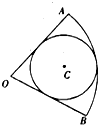 如图圆C内切于扇形AOB,∠AOB=
如图圆C内切于扇形AOB,∠AOB=| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为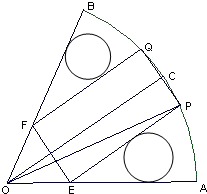 如图,在半径为R、圆心角为
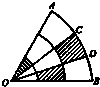
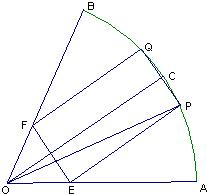
如图,在半径为R、圆心角为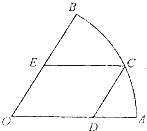 (2013•南京二模)如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在
(2013•南京二模)如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在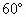 ,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图),则OC的长为________.
,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图),则OC的长为________.