题目内容
已知函数(1)求f(x)的最小正周期; (2)
(3)在(2)的条件下,求满足f(x)=1,
解析: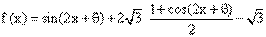 =
=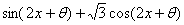 =
=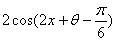
(1)
(2)由f(x)为偶函数得f(-x)=f(x)对任意x∈R成立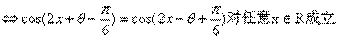 ①
①
在①中令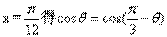 ∴
∴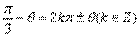 注意到
注意到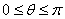 ,故这里k=0,由此解得
,故这里k=0,由此解得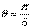 .
.
(3)当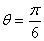 时,f(x)=2cos2x ∴由f(x)=1得,2cos2x=1
时,f(x)=2cos2x ∴由f(x)=1得,2cos2x=1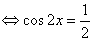 ②
②
注意到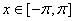 ,∴由②得
,∴由②得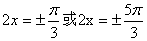 , 即
, 即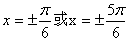
∴所求x的集合为{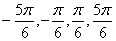 }.
}.
(1)
(2)由f(x)为偶函数得f(-x)=f(x)对任意x∈R成立
在①中令
(3)当
注意到
∴所求x的集合为{

练习册系列答案
相关题目