题目内容
已知三次函数f(x)=ax3+bx2+cx(a,b,c∈R).(1)若函数f(x)过点(-1,2)且在点(1,f(1))处的切线方程为y+2=0,求函数f(x)的解析式;
(2)当a=1时,若-2≤f(-1)≤1,-1≤f(1)≤3,试求f(2)的取值范围;
(3)对?x∈[-1,1],都有|f′(x)|≤1,试求实数a的最大值,并求a取得最大值时f(x)的表达式.
【答案】分析:(1)由题意可得f(-1)=-a+b-c=2,①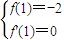 ,即
,即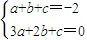 ②,由①②可解得得a、b、c的值,可写解析式;
②,由①②可解得得a、b、c的值,可写解析式;
(2)由f(1)=1+b+c,f(-1)=-1+b-c可知f(2)=8+4b+2c=3f(1)+f(-1)+6,求得-2≤f(-1)≤1,-1≤f(1)≤3整体利用可求f(2)的范围;
(3)?x∈[-1,1],都有|f′(x)|≤1,可知|f′(-1)|≤1,|f′(0)|≤1,|f′(1)|≤1,及6a=f′(-1)+f′(1)-2f′(0)可求a的最大值 ,由此可解bc的值,即得答案.
,由此可解bc的值,即得答案.
解答:解:(1)∵函数f(x)过点(1,-2),∴f(-1)=-a+b-c=2,①
由f′(x)=3ax2+2bx+c,函数f(x)在点(1,f(1))处的切线方程为:y+2=0
∴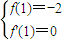 ,∴
,∴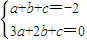 ,②
,②
由①和②解得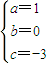 ,故f(x)=x3-3x;
,故f(x)=x3-3x;
(2)当a=1时,f(x)=x3+bx2+cx,∴f(1)=1+b+c,f(-1)=-1+b-c
可得:c=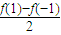 -1,b=
-1,b=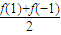 ∴f(2)=8+4b+2c=3f(1)+f(-1)+6
∴f(2)=8+4b+2c=3f(1)+f(-1)+6
又由题意-2≤f(-1)≤1,-1≤f(1)≤3,∴-3≤3f(1)≤9,
故1≤3f(1)+f(-1)+6≤16,
即1≤f(2)≤16.
(3)∵f′(x)=3ax2+2bx+c,则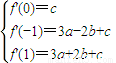 ,可得6a=f′(-1)+f′(1)-2f′(0)
,可得6a=f′(-1)+f′(1)-2f′(0)
∵当-1≤x≤1时,|f′(x)|≤1,∴|f′(-1)|≤1,|f′(0)|≤1,|f′(1)|≤1
∴6|a|=|f′(-1)+f′(1)-2f′(0)|≤|f′(-1)+f′(1)+2f′(0)|≤4
∴a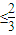 ,故a的最大值
,故a的最大值 ,
,
当a= 时,
时,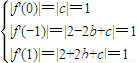 ,解得
,解得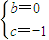 ,
,
∴a取得最大值时f(x)= x3-x.
x3-x.
点评:本题为导数和不等式的综合应用,涉及整体代入法求取值范围,属中档题.
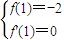 ,即
,即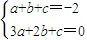 ②,由①②可解得得a、b、c的值,可写解析式;
②,由①②可解得得a、b、c的值,可写解析式;(2)由f(1)=1+b+c,f(-1)=-1+b-c可知f(2)=8+4b+2c=3f(1)+f(-1)+6,求得-2≤f(-1)≤1,-1≤f(1)≤3整体利用可求f(2)的范围;
(3)?x∈[-1,1],都有|f′(x)|≤1,可知|f′(-1)|≤1,|f′(0)|≤1,|f′(1)|≤1,及6a=f′(-1)+f′(1)-2f′(0)可求a的最大值
 ,由此可解bc的值,即得答案.
,由此可解bc的值,即得答案.解答:解:(1)∵函数f(x)过点(1,-2),∴f(-1)=-a+b-c=2,①
由f′(x)=3ax2+2bx+c,函数f(x)在点(1,f(1))处的切线方程为:y+2=0
∴
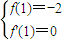 ,∴
,∴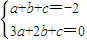 ,②
,②由①和②解得
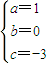 ,故f(x)=x3-3x;
,故f(x)=x3-3x;(2)当a=1时,f(x)=x3+bx2+cx,∴f(1)=1+b+c,f(-1)=-1+b-c
可得:c=
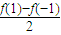 -1,b=
-1,b=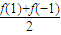 ∴f(2)=8+4b+2c=3f(1)+f(-1)+6
∴f(2)=8+4b+2c=3f(1)+f(-1)+6又由题意-2≤f(-1)≤1,-1≤f(1)≤3,∴-3≤3f(1)≤9,
故1≤3f(1)+f(-1)+6≤16,
即1≤f(2)≤16.
(3)∵f′(x)=3ax2+2bx+c,则
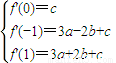 ,可得6a=f′(-1)+f′(1)-2f′(0)
,可得6a=f′(-1)+f′(1)-2f′(0)∵当-1≤x≤1时,|f′(x)|≤1,∴|f′(-1)|≤1,|f′(0)|≤1,|f′(1)|≤1
∴6|a|=|f′(-1)+f′(1)-2f′(0)|≤|f′(-1)+f′(1)+2f′(0)|≤4
∴a
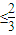 ,故a的最大值
,故a的最大值 ,
,当a=
 时,
时,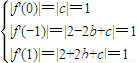 ,解得
,解得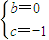 ,
,∴a取得最大值时f(x)=
 x3-x.
x3-x.点评:本题为导数和不等式的综合应用,涉及整体代入法求取值范围,属中档题.

练习册系列答案
相关题目
 已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则
已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则