Question

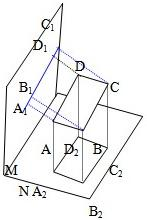
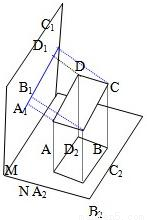
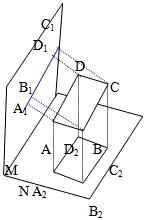已知空间四点A、B、C、D和两平面M、N，又知A、B、C、D在M内的射影A₁B₁C₁D₁是一条直线，在N内的射影A₂B₂C₂D₂是一个平行四边形，求证ABCD是一个平行四边形．

Answer 1

证明：（1）先证A、B、C、D四点共面
设通过直线A₁B₁C₁D₁而垂直于平面M的平面为P
则因AA₁⊥平面M，而A₁又在直线A₁B₁C₁D₁上，
所以点A在平面P内，同理点B、C、D均在平面P内，
即A、B、C、D四点共面
（2）证ABCD是一个平行四边形
若AB与DC相交于E，
则其在平面N内的射影A₂B₂与D₂C₂也相交于E₂，
此与A₂B₂∥D₂C₂的假设相违，所以AB∥DC，同理AD∥BC
故ABCD是一个平行四边形．
分析：利用两个平面垂直的性质：若两个平面垂直，通过一个平面中的一点垂直于另一个平面的直线在第一个平面内；证出四点共面；通过反证法证出四边形的两条对边不能相交即两对边平行，命题得证．
点评：本题考查两平面垂直的性质：若两个平面垂直，通过一个平面中的一点垂直于另一个平面的直线在第一个平面内、反证法在证题中的应用．