题目内容
某厂生产产品x件的总成本c(x)=1200+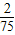 x3(万元),已知产品单价P(万元)与产品件数x满足:p2=
x3(万元),已知产品单价P(万元)与产品件数x满足:p2=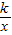 ,生产100件这样的产品单价为50万元.
,生产100件这样的产品单价为50万元.(1)设产量为x件时,总利润为L(x)(万元),求L(x)的解析式;
(2)产量x定为多少件时总利润L(x)(万元)最大?并求最大值(精确到1万元).
【答案】分析:(1)由题可知生产100件这样的产品单价为50万元,所以把x=100,P=50代入到p2=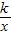 中求出k的值确定出P的解析式,然后根据总利润=总销售额-总成本得出L(x)即可;
中求出k的值确定出P的解析式,然后根据总利润=总销售额-总成本得出L(x)即可;
(2)令L′(x)=0求出x的值,此时总利润最大,最大利润为L(25).
解答:解:(1)由题意有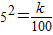 ,解得k=25×104,∴
,解得k=25×104,∴ ,
,
∴总利润 =
= ;
;
(2)由(1)得 ,令
,令 ,
,
令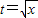 ,得
,得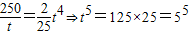 ,∴t=5,于是x=t2=25,
,∴t=5,于是x=t2=25,
则x=25,所以当产量定为25时,总利润最大.
这时L(25)≈-416.7+2500-1200≈883.
答:产量x定为25件时总利润L(x)最大,约为883万元.
点评:考查学生根据实际问题选择函数关系的能力,及利用导数求函数最值的方法的能力.
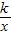 中求出k的值确定出P的解析式,然后根据总利润=总销售额-总成本得出L(x)即可;
中求出k的值确定出P的解析式,然后根据总利润=总销售额-总成本得出L(x)即可;(2)令L′(x)=0求出x的值,此时总利润最大,最大利润为L(25).
解答:解:(1)由题意有
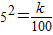 ,解得k=25×104,∴
,解得k=25×104,∴ ,
,∴总利润
 =
= ;
;(2)由(1)得
 ,令
,令 ,
,令
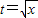 ,得
,得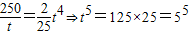 ,∴t=5,于是x=t2=25,
,∴t=5,于是x=t2=25,则x=25,所以当产量定为25时,总利润最大.
这时L(25)≈-416.7+2500-1200≈883.
答:产量x定为25件时总利润L(x)最大,约为883万元.
点评:考查学生根据实际问题选择函数关系的能力,及利用导数求函数最值的方法的能力.

练习册系列答案
相关题目
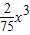 (万元),已知产品单价P(万元)与产品件数x满足:P2=
(万元),已知产品单价P(万元)与产品件数x满足:P2=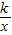 ,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?
,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?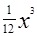 (万元),已知产品单价P(万元) 与产品件数x满足:
(万元),已知产品单价P(万元) 与产品件数x满足: ,生产1件这样的产品单价为16万元.
,生产1件这样的产品单价为16万元.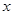 件时,总利润为
件时,总利润为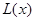 (万元),求
(万元),求