题目内容
在函数y=logax(a>1)的图象上有A、B、C三点,横坐标分别为m,m+2,m+4,其中m>1.
(1)求△ABC的面积S=f(m)的表达式;
(2)求S=f(m)的值域.
(1)求△ABC的面积S=f(m)的表达式;
(2)求S=f(m)的值域.
分析:(1)分别由A、B、C三点向x轴作垂线,交点为D,E,F,根据S△ABC=SABED+SBCFE-SACFD和D,E,F的坐标,进而得出函数f(m)的表达式.
(2)由(1)中得S=f(m)=loga
(m>1),先根据 m>1,推断t=m2+4m为增函数,进而推断函数f(m)为减函数,根据m的范围,求得函数的值域.
(2)由(1)中得S=f(m)=loga
| (m+2)2 |
| m2+4m |
解答:解:(1)解:分别由A、B、C三点向x轴作垂线,交点为D,E,F,如图: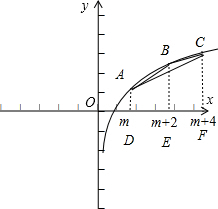
S△ABC=SABED+SBCFE-SACFD
=
•2•{[logam+loga(m+2)]+[loga(m+2)+loga(m+4)]}-2•[logam+loga(m+4)]
=2loga(m+2)-logam-loga(m+4)
=loga
(m>1)
∴S=f(m)=loga
(m>1)
(2)∵s=f(m)=loga(1+
) (m>1)
m>1时,t=m2+4m为增函数,a>1,
∴S=f(m)在(1,+∞)上为减函数,
∴1<1+
<1+
=
,
∴0<S<loga
,
∴S=f(m)的值域为(0,loga
)

S△ABC=SABED+SBCFE-SACFD
=
| 1 |
| 2 |
=2loga(m+2)-logam-loga(m+4)
=loga
| (m+2)2 |
| m(m+4) |
∴S=f(m)=loga
| (m+2)2 |
| m2+4m |
(2)∵s=f(m)=loga(1+
| 4 |
| m2+4m |
m>1时,t=m2+4m为增函数,a>1,
∴S=f(m)在(1,+∞)上为减函数,
∴1<1+
| 4 |
| m2+4m |
| 4 |
| 5 |
| 9 |
| 5 |
∴0<S<loga
| 9 |
| 5 |
∴S=f(m)的值域为(0,loga
| 9 |
| 5 |
点评:本题主要考查了对数函数的图象和性质,建立函数模型,利用函数单调性求函数的值域和最值等问题,复合函数单调性问题,属中档题

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目