题目内容
已知不等式 ,若对任意
,若对任意 且
且 ,该不等式恒成立,则实数
,该不等式恒成立,则实数 的取值范围是 .
的取值范围是 .
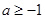 .
.
解析试题分析:由题意可知:不等式xy≤ax2+2y2对于x∈[1,2],y∈[2,3]恒成立,
即:a≥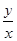 -2(
-2(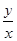 )2,对于x∈[1,2],y∈[2,3]恒成立,
)2,对于x∈[1,2],y∈[2,3]恒成立,
令 t=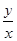 ,则1≤t≤3,∴a≥t-2t2在[1,3]上恒成立,
,则1≤t≤3,∴a≥t-2t2在[1,3]上恒成立,
∵y=-2t2+t=-2(t- )2+
)2+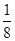
∴ymax=-1,
∴a≥-1。
考点:主要主要考查函数恒成立问题,分离参数法的应用,二次函数在闭区间上的值域。
点评:中档题,本题综合性较强。一般的,函数恒成立问题,往往要转化成求函数的最值问题。分离参数法是处理此类问题的常用方法。

练习册系列答案
相关题目
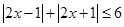 的解集为________
的解集为________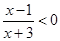 的解集是 .
的解集是 . 的解集不是空集,则实数a的取值范围为______.
的解集不是空集,则实数a的取值范围为______. 的解集为_____.
的解集为_____.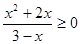 的解集为 .
的解集为 . 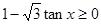 的解集是 .
的解集是 .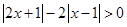 的解集为_______________.
的解集为_______________. 中,三内角
中,三内角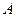 、
、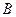 、
、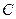 所对边的长分别为
所对边的长分别为 、
、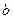 、
、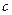 ,已知
,已知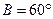 ,
,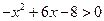 的解集为
的解集为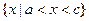 ,则
,则 ___▲___.
___▲___.