题目内容
若命题甲为: 成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( )
成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( )A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既不充分也不必要条件
【答案】分析:根据等差中项和等比中项列式,结合充分必要条件的定义加以判断,不难得到甲是乙的充要条件.
解答:解:充分性
若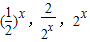 成等比数列,则
成等比数列,则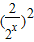 =
= •2x
•2x
∴22-2x=1,解之得x=1
此时,数列lgx,lg(x+1),lg(x+3)为lg1,lg2,lg4,满足成等差数列
所以充分性成立;
必要性
若lgx,lg(x+1),lg(x+3)成等差数列,则2lg(x+1)=lgx+lg(x+3)
即(x+1)2=x(x+3),解之得x=1
此时,数列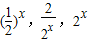 为
为 ,1,2,满足成等比数列
,1,2,满足成等比数列
所以必要性成立.
故选:C
点评:本题给出有关数列的两个命题,要我们判断两个命题间的充要关系,着重考查了等差中项、等比中项和充分必要条件的判断等知识,属于基础题.
解答:解:充分性
若
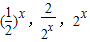 成等比数列,则
成等比数列,则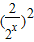 =
= •2x
•2x∴22-2x=1,解之得x=1
此时,数列lgx,lg(x+1),lg(x+3)为lg1,lg2,lg4,满足成等差数列
所以充分性成立;
必要性
若lgx,lg(x+1),lg(x+3)成等差数列,则2lg(x+1)=lgx+lg(x+3)
即(x+1)2=x(x+3),解之得x=1
此时,数列
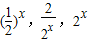 为
为 ,1,2,满足成等比数列
,1,2,满足成等比数列所以必要性成立.
故选:C
点评:本题给出有关数列的两个命题,要我们判断两个命题间的充要关系,着重考查了等差中项、等比中项和充分必要条件的判断等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( )
成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( ) 成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( )
成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( )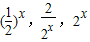 成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( )
成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( ) 成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( )
成等比数列,命题乙为:lgx,lg(x+1),lg(x+3)成等差数列,则甲是乙的( )