题目内容
已知数列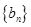 是首项为1,公差为2的等差数列,数列
是首项为1,公差为2的等差数列,数列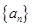 的前n项和
的前n项和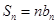 .
.
(I)求数列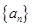 的通项公式;
的通项公式;
(II)设 , 求数列
, 求数列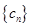 的前n项和
的前n项和 .
.
【答案】
(Ⅰ)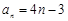 .(Ⅱ)由(Ⅰ)
.(Ⅱ)由(Ⅰ)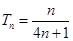 .
.
【解析】
试题分析:(Ⅰ)根据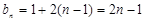 .得到
.得到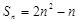 .
.
从而通过确定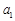 ,当
,当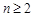 时,
时,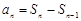 ,验证
,验证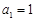 也适合上式,得到所求通项公式.
也适合上式,得到所求通项公式.
(Ⅱ)利用“裂项相消法”求和.难度不大,对基础知识的考查较为全面.
试题解析:(Ⅰ)由已知,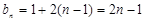 .
2分
.
2分
所以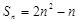 .从而
.从而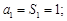
当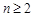 时,
时,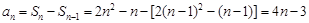 ,
,
又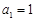 也适合上式,所以
也适合上式,所以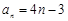 .
6分
.
6分
(Ⅱ)由(Ⅰ)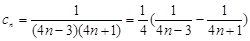 , 8分
, 8分
所以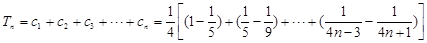
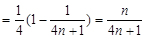 .
12分
.
12分
考点:等差数列的通项公式,裂项相消法.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
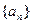 是首项为1的等差数列,且公差不为零,而等比数列
是首项为1的等差数列,且公差不为零,而等比数列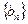 的前三项分别是
的前三项分别是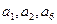 。
。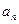
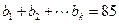 ,求正整数
,求正整数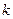 的值。
的值。 是首项为1的等差数列,且
是首项为1的等差数列,且 ,若
,若 成等比数列,(1)求数列
成等比数列,(1)求数列 ,求数列
,求数列 的前
的前 项和
项和 .
. 是首项为1的等差数列,且
是首项为1的等差数列,且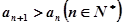 , 若
, 若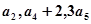
 ,求数列
,求数列 的前
的前 项和
项和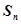 .
.