题目内容
已知椭圆C: 的离心率为
的离心率为 ,过右顶点A的直线l与椭圆C相交于A,B两点,且B(-1,-3),
,过右顶点A的直线l与椭圆C相交于A,B两点,且B(-1,-3),
(Ⅰ)求椭圆C和直线l的方程;
(Ⅱ)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D,若曲线x2-2mx+y2+4y+m2-4=0与区域D有公共点,试求实数m的最小值。
 的离心率为
的离心率为 ,过右顶点A的直线l与椭圆C相交于A,B两点,且B(-1,-3),
,过右顶点A的直线l与椭圆C相交于A,B两点,且B(-1,-3),(Ⅰ)求椭圆C和直线l的方程;
(Ⅱ)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D,若曲线x2-2mx+y2+4y+m2-4=0与区域D有公共点,试求实数m的最小值。

解:(Ⅰ)由离心率e=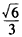 ,得
,得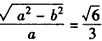 ,
,
即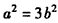 ,①
,①
又点B(-1,-3)在椭圆C: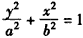 上,即
上,即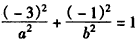 ,②
,②
解①②得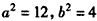 ,
,
故所求椭圆方程为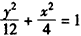 ,
,
由A(2,0),B(-1,-3)得直线l的方程为y=x-2。
(Ⅱ)曲线x2-2mx+y2+4y+m2-4=0,
即圆(x-m)2+(y+2)2=8,其圆心坐标为G(m,-2),半径r=2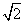 ,表示圆心在直线y=-2上,半径为2
,表示圆心在直线y=-2上,半径为2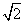 的动圆,
的动圆,
要求实数m的最小值,由下图可知,只须考虑m<0的情形.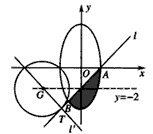
设圆G与直线l相切于点T,则由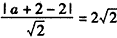 ,得m=±4,
,得m=±4,
当m=-4时,过点G(-4,-2)与直线l垂直的直线l′的方程为x+y+6=0,
解方程组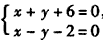 ,得T(-2,-4),
,得T(-2,-4),
因为区域D内的点的横坐标的最小值与最大值分别为-1,2,
所以切点T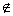 D,
D,
由图可知当圆G过点B时,m取得最小值,
即(-1-m)2+(-3+2)2=8,解得mmin=-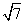 -1。
-1。

练习册系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、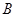 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.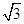
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线