题目内容
已知函数f(x)=2
sinxcosx-2cosx-2cos2x+1
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)在△ABC中,若f(
)=2,b=1,c=2,求a的值.
| 3 |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)在△ABC中,若f(
| A |
| 2 |
(Ⅰ)f(x)=2
sinxcosx-2cosx-2cos2x+1
=
sin2x-cos2x
=2sin(2x-
),
∴函数f(x)的最小正周期T=π;
(Ⅱ)∵f(
)=2,
∴2sin(A-
)=2,即sin(A-
)=1,
∴A-
=
+2kπ,A=
+2kπ,k∈Z,
又0<A<π,
∴A=
,
又在△ABC中,b=1,c=2,
由余弦定理得:a2=b2+c2-2bccosA=1+4-2×1×2×(-
)=7,
解得:a=
.
| 3 |
=
| 3 |
=2sin(2x-
| π |
| 6 |
∴函数f(x)的最小正周期T=π;
(Ⅱ)∵f(
| A |
| 2 |
∴2sin(A-
| π |
| 6 |
| π |
| 6 |
∴A-
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
又0<A<π,
∴A=
| 2π |
| 3 |
又在△ABC中,b=1,c=2,
由余弦定理得:a2=b2+c2-2bccosA=1+4-2×1×2×(-
| 1 |
| 2 |
解得:a=
| 7 |

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
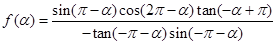
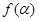 ;
;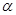 是第三象限角,且cos(
是第三象限角,且cos(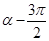 )=
)=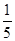 ,求
,求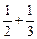 +…+
+…+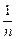 ,(n∈N*)设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-
,(n∈N*)设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-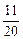 [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立.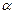 的顶点在原点,始边与
的顶点在原点,始边与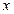 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点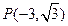
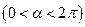 .
.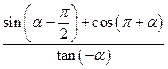 的值;
的值;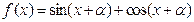 (
(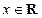 )的图像关于直线
)的图像关于直线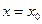 对称,求
对称,求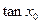 的值.
的值. 中,
中, ,
, ,则
,则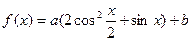 。
。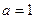 时,求
时,求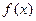 的单调递增区间:
的单调递增区间: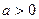 ,且
,且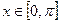 时,
时,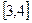 ,求
,求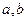 的值。
的值。 ,则
,则



