题目内容
两条互相平行的直线分别过点A(6,2)和B(-3,-1),并且各自绕着A,B旋转,如果两条平行直线间的距离为d.
求:
(1)d的变化范围;
(2)当d取最大值时两条直线的方程.
求:
(1)d的变化范围;
(2)当d取最大值时两条直线的方程.
分析:(1)方法一:①当两条直线的斜率不存在时,可求得两直线间的距离;②当两条直线的斜率存在时,设这两条直线方程为l1:y-2=k(x-6),l2:y+1=k(x+3),利用两平行线间的距离公式可求得两直线间的距离d的表示式,两端平方,整理成关于斜率k的二次方程,利用其有解的条件即可求得d的变化范围;
(2)作出图形,数形结合即可求得答案.
(2)作出图形,数形结合即可求得答案.
解答:解:(1)方法一:①当两条直线的斜率不存在时,即两直线分别为x=6和x=-3,则它们之间的距离为9.…(2分)
②当两条直线的斜率存在时,设这两条直线方程为
l1:y-2=k(x-6),l2:y+1=k(x+3),
即l1:kx-y-6k+2=0,l2:kx-y+3k-1=0,…(4分)
∴d=
=
.
即(81-d2)k2-54k+9-d2=0.
∵k∈R,且d≠9,d>0,
∴△=(-54)2-4(81-d2)(9-d2)≥0,即0<d≤3
且d≠9.…(9分)
综合①②可知,所求d的变化范围为(0,3
].
方法二:如图所示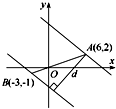 ,显然有0<d≤|AB|.
,显然有0<d≤|AB|.
而|AB|=
=3
.
故所求的d的变化范围为(0,3
].
(2)由图可知,当d取最大值时,两直线垂直于AB.
而kAB=
=
,
∴所求直线的斜率为-3.故所求的直线方程分别为
y-2=-3(x-6),y+1=-3(x+3),即3x+y-20=0和3x+y+10=0-…(13分)
②当两条直线的斜率存在时,设这两条直线方程为
l1:y-2=k(x-6),l2:y+1=k(x+3),
即l1:kx-y-6k+2=0,l2:kx-y+3k-1=0,…(4分)
∴d=
| |3k-1+6k-2| | ||
|
| 3|3k-1| | ||
|
即(81-d2)k2-54k+9-d2=0.
∵k∈R,且d≠9,d>0,
∴△=(-54)2-4(81-d2)(9-d2)≥0,即0<d≤3
| 10 |
综合①②可知,所求d的变化范围为(0,3
| 10 |
方法二:如图所示
 ,显然有0<d≤|AB|.
,显然有0<d≤|AB|.而|AB|=
| [6-(-3)]2+[2-(-1)]2 |
| 10 |
故所求的d的变化范围为(0,3
| 10 |
(2)由图可知,当d取最大值时,两直线垂直于AB.
而kAB=
| 2-(-1) |
| 6-(-3) |
| 1 |
| 3 |
∴所求直线的斜率为-3.故所求的直线方程分别为
y-2=-3(x-6),y+1=-3(x+3),即3x+y-20=0和3x+y+10=0-…(13分)
点评:本题考查两条平行直线间的距离,考查分类讨论思想与数形结合思想的综合运用,属于难题.

练习册系列答案
相关题目
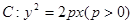 过点
过点 。
。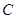 的标准方程,并求其准线方程;
的标准方程,并求其准线方程;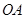 (
(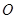 为坐标原点)的直线
为坐标原点)的直线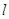 ,使得直线
,使得直线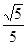 ?
?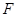 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线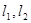 ,设
,设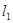 与抛物线
与抛物线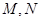 ,
, 与抛物线
与抛物线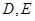 ,求
,求 的最小值。
的最小值。