题目内容
(2013•嘉兴一模)己知抛物线y2=4x的焦点为F,若点A,B是该抛物线上的点,∠AFB=
,线段AB的中点M在抛物线的准线上的射影为N,则
的最大值为
.
| π |
| 2 |
| |MN| |
| |AB| |
| ||
| 2 |
| ||
| 2 |
分析:设|AF|=a、|BF|=b,由抛物线定义结合梯形的中位线定理,得2|MN|=a+b.再由勾股定理得|AB|2=a2+b2,结合基本不等式求得|AB|的范围,从而可得
的最大值.
| |MN| |
| |AB| |
解答:解:设|AF|=a,|BF|=b,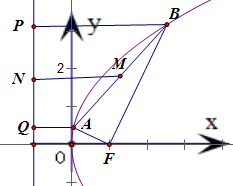 A、B在准线上的射影点分别为Q、P,连接AQ、BQ
A、B在准线上的射影点分别为Q、P,连接AQ、BQ
由抛物线定义,得AF|=|AQ|且|BF|=|BP|
在梯形ABPQ中根据中位线定理,得2|MN|=|AQ|+|BP|=a+b.
由勾股定理得|AB|2=a2+b2,配方得|AB|2=(a+b)2-2ab,
又∵ab≤(
) 2,
∴(a+b)2-2ab≥(a+b)2-2×(
) 2=
(a+b)2
得到|AB|≥
(a+b).
所以
≤
=
,即
的最大值为
.
故答案为:
 A、B在准线上的射影点分别为Q、P,连接AQ、BQ
A、B在准线上的射影点分别为Q、P,连接AQ、BQ 由抛物线定义,得AF|=|AQ|且|BF|=|BP|
在梯形ABPQ中根据中位线定理,得2|MN|=|AQ|+|BP|=a+b.
由勾股定理得|AB|2=a2+b2,配方得|AB|2=(a+b)2-2ab,
又∵ab≤(
| a+b |
| 2 |
∴(a+b)2-2ab≥(a+b)2-2×(
| a+b |
| 2 |
| 1 |
| 2 |
得到|AB|≥
| ||
| 2 |
所以
| |MN| |
| |AB| |
| ||||
|
| ||
| 2 |
| |MN| |
| |AB| |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题给出抛物线的弦AB对焦点F所张的角为直角,求AB中点M到准线的距离与AB比值的取值范围,着重考查了抛物线的定义与简单几何性质、梯形的中位线定理和基本不等式求最值等知识,属于中档题.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 (2013•嘉兴一模)如图,直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=
(2013•嘉兴一模)如图,直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD= (2013•嘉兴一模)一个几何体的三视图如图所示,则该几何体的体积为
(2013•嘉兴一模)一个几何体的三视图如图所示,则该几何体的体积为