题目内容
 如图,由曲线y=x2-1,直线x=0,x=2和x轴围成的封闭图形的面积是( )
如图,由曲线y=x2-1,直线x=0,x=2和x轴围成的封闭图形的面积是( )分析:y=x2-1,直线x=0,x=2和x轴围成的封闭图形,然后利用定积分表示区域面积,然后利用定积分的定义进行求解即可.
解答:解:由曲线y=x2-1,直线x=0,x=2和x轴围成的封闭图形的面积为
S=∫01(1-x2)dx+∫12(x2-1)dx
=(x-
x3)|01+(
x3-x)|12
=
+
-2-
+1
=2
故选D.
S=∫01(1-x2)dx+∫12(x2-1)dx
=(x-
| 1 |
| 3 |
| 1 |
| 3 |
=
| 2 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
=2
故选D.
点评:本题主要考查了利用定积分求面积,同时考查了定积分的等价转化,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
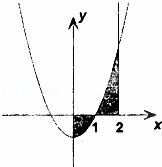
如图,由曲线y=x2﹣1,直线x=0,x=2和x轴围成的封闭图形的面积为( )
|
| A. |
| B. | 1 | C. | 2 | D. | 3 |
 如图,由曲线y=x2-1,直线x=0,x=2和x轴围成的封闭图形的面积为( )
如图,由曲线y=x2-1,直线x=0,x=2和x轴围成的封闭图形的面积为( )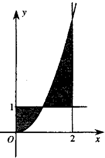 如图,由曲线y=x2(x≥0)和直线x=0,x=2,y=1所围成的图形(阴影部分)的面积是
如图,由曲线y=x2(x≥0)和直线x=0,x=2,y=1所围成的图形(阴影部分)的面积是