题目内容
①任取x∈R都有3x>2x;
②当a>1时,任取x∈R都有ax>a-x;
③y=(
)-x是增函数;
④y=2|x|的最小值为1;
⑤在同一坐标系中,y=x3与y=x
的图象关于y=x对称.
以上说法正确的是
②当a>1时,任取x∈R都有ax>a-x;
③y=(
| 3 |
④y=2|x|的最小值为1;
⑤在同一坐标系中,y=x3与y=x
| 1 |
| 3 |
以上说法正确的是
④⑤
④⑤
.分析:举出反例x=0,可判断①②的真假;根据指数函数单调性与底数的关系,可判断③的真假;根据指数函数的图象和性质,求出y=2|x|的最小值,可判断④的真假;根据互为反函数的两个函数的图象关于y=x对称,可判断⑤
解答:解:当x=0时,3x>2x不成立,故①错误;
当x=0时,ax>a-x不成立,故②错误;
y=(
)-x=(
)x为减函数,故③错误;
当x=0时,y=2|x|的最小值为1,故④正确;
y=x3与y=x
互为反函数,故在同一坐标系中,图象关于y=x对称,故⑤正确.
故答案为:④⑤
当x=0时,ax>a-x不成立,故②错误;
y=(
| 3 |
| ||
| 3 |
当x=0时,y=2|x|的最小值为1,故④正确;
y=x3与y=x
| 1 |
| 3 |
故答案为:④⑤
点评:本题以命题的真假判断为载体,考查了指数函数的图象和性质,反函数的图象关系,是函数图象和性质的简单综合考查,难度不大.

练习册系列答案
相关题目
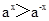
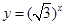 是增函数
是增函数 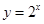 与
与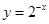 的图象对称于y轴
的图象对称于y轴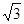 )-x是增函数
)-x是增函数