题目内容
某几何体的主视图与俯视图如图所示，左视图与主视图相同，且图中的四边形都是边长为2的正方形，，两条虚线互相垂直，则该几何体的体积为（ ）
A 
B.
C. 6 D. 4
A
解析试题分析：根据三视图，还原成几何体，再根据长度关系，即可求得几何体的体积解：由三视图知，原几何体为一个正方体挖掉一个正四棱锥,其中正方体的棱为2，正四棱柱的底面边长为正方体的上底面，高为1,∴原几何体的体积为V=2×2×2-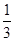
×2×2×1=故选A
考点：三视图
点评：本题考查三视图，要求能把三视图还原成原几何体，有比较好的空间想象力，能根据三视图找到原几何体中的垂直平行关系和长度关系．属简单题
练习册系列答案
相关题目
棱长都是1的三棱锥的表面积为（ ）
A． | B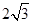． | C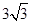． | D． |
如图是水平放置的平面图形的斜二测直观图，其原来平面图形面积是（ ）
A．2 | B．4 | C．4 | D．8 |
若某空间几何体的三视图如图所示，则该几何体的体积是（ ）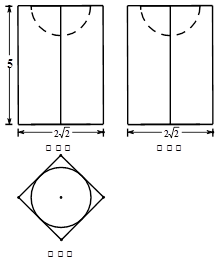
| A．20-2π | B． | C． | D． |
某几何体的三视图如下，则几何体的表面积为（ ）
A．28+6 | B．30+6 | C．56+12 | D．60+12 |
已知正三棱柱底面边长是2，，外接球的表面积是
，则该三棱柱的侧棱长（ ）.
A． | B． | C． | D． |
、
、
、
四点，若
，则四面体
的体积的取值范围是
