题目内容
若不等式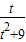 ≤a≤
≤a≤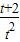 在t∈(0,2]上恒成立,则a的取值范围是( )
在t∈(0,2]上恒成立,则a的取值范围是( )A.[
 ,1]
,1]B.[
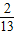 ,1]
,1]C.[
 ,
,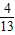 ]
]D.[
 ,2
,2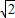 ]
]
【答案】分析:由基本不等式,算出函数y=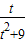 在区间(0,2]上为增函数,得到t=2时,
在区间(0,2]上为增函数,得到t=2时,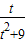 的最大值为
的最大值为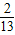 ;根据二次函数的性质,算出t=2时
;根据二次函数的性质,算出t=2时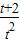 的最小值为1.由此可得原不等式恒成立时,a的取值范围是[
的最小值为1.由此可得原不等式恒成立时,a的取值范围是[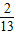 ,1].
,1].
解答:解:∵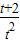 =
= +
+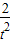 ,在t∈(0,2]上为减函数
,在t∈(0,2]上为减函数
∴当t=2时,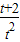 的最小值为1;
的最小值为1;
又∵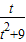 ≤
≤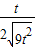 =
= ,当且仅当t=3时等号成立
,当且仅当t=3时等号成立
∴函数y=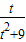 在区间(0,2]上为增函数
在区间(0,2]上为增函数
可得t=2时,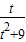 的最大值为
的最大值为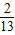
∵不等式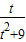 ≤a≤
≤a≤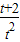 在t∈(0,2]上恒成立,
在t∈(0,2]上恒成立,
∴(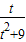 )max≤a≤(
)max≤a≤(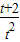 )min,即
)min,即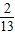 ≤a≤1
≤a≤1
可得a的取值范围是[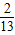 ,1]
,1]
点评:本题给出不等式恒成立,求参数a的取值范围.着重考查了基本不等式、函数的单调性、函数最值的求法和不等式恒成立的处理等知识,属于中档题.
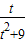 在区间(0,2]上为增函数,得到t=2时,
在区间(0,2]上为增函数,得到t=2时,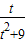 的最大值为
的最大值为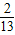 ;根据二次函数的性质,算出t=2时
;根据二次函数的性质,算出t=2时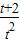 的最小值为1.由此可得原不等式恒成立时,a的取值范围是[
的最小值为1.由此可得原不等式恒成立时,a的取值范围是[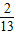 ,1].
,1].解答:解:∵
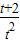 =
= +
+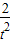 ,在t∈(0,2]上为减函数
,在t∈(0,2]上为减函数∴当t=2时,
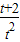 的最小值为1;
的最小值为1;又∵
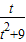 ≤
≤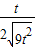 =
= ,当且仅当t=3时等号成立
,当且仅当t=3时等号成立∴函数y=
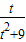 在区间(0,2]上为增函数
在区间(0,2]上为增函数可得t=2时,
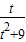 的最大值为
的最大值为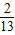
∵不等式
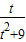 ≤a≤
≤a≤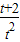 在t∈(0,2]上恒成立,
在t∈(0,2]上恒成立,∴(
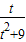 )max≤a≤(
)max≤a≤(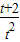 )min,即
)min,即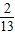 ≤a≤1
≤a≤1可得a的取值范围是[
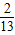 ,1]
,1]点评:本题给出不等式恒成立,求参数a的取值范围.着重考查了基本不等式、函数的单调性、函数最值的求法和不等式恒成立的处理等知识,属于中档题.

练习册系列答案
相关题目
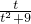 ≤a≤
≤a≤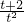 在t∈(0,2]上恒成立,则a的取值范围是
在t∈(0,2]上恒成立,则a的取值范围是 ,1]
,1]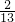 ,1]
,1]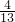 ]
] ]
]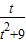 ≤a≤
≤a≤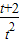 在t∈(0,2]上恒成立,则a的取值范围是( )
在t∈(0,2]上恒成立,则a的取值范围是( ) ,1]
,1]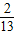 ,1]
,1] ,
,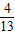 ]
] ,2
,2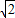 ]
]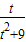 ≤a≤
≤a≤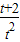 在t∈(0,2]上恒成立,则a的取值范围是( )
在t∈(0,2]上恒成立,则a的取值范围是( ) ,1]
,1]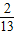 ,1]
,1] ,
,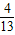 ]
] ,2
,2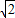 ]
]